题目内容
曲线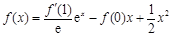 在点
在点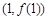 处的切线方程为_________.
处的切线方程为_________.
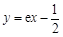
解析试题分析:显然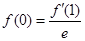 ,对
,对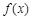 求导得
求导得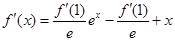 ,在此式中令
,在此式中令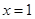 ,得
,得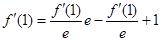 ,解得
,解得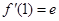 ,所以
,所以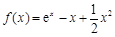 ,
,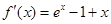 ,得
,得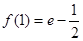 所以所求的曲线在点
所以所求的曲线在点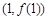 处的切线方程为
处的切线方程为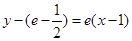 ,即
,即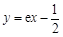 .
.
考点:函数的导数、曲线的切线.

练习册系列答案
 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案
相关题目
题目内容
曲线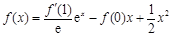 在点
在点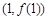 处的切线方程为_________.
处的切线方程为_________.
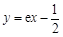
解析试题分析:显然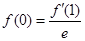 ,对
,对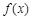 求导得
求导得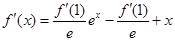 ,在此式中令
,在此式中令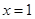 ,得
,得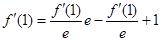 ,解得
,解得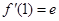 ,所以
,所以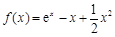 ,
,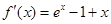 ,得
,得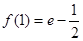 所以所求的曲线在点
所以所求的曲线在点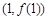 处的切线方程为
处的切线方程为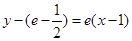 ,即
,即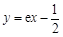 .
.
考点:函数的导数、曲线的切线.

 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案