题目内容
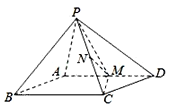
【题目】如图，在四棱锥
中，平面
平面
.四边形为正方形，且
为
的中点，
为
的中点.
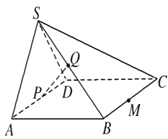
（1）求证：
平面
；
（2）求证：
平面
.
【答案】(1)见解析(2)见解析
【证明】：(1)因为四边形ABCD为正方形，所以CD⊥AD.
又平面SAD⊥平面ABCD，且平面SAD∩平面ABCD＝AD，
所以CD⊥平面SAD.
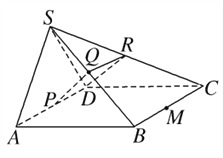
(2)取SC的中点R，连接QR，DR.
由题意知，PD∥BC且PD＝
BC.
在△SBC中，Q为SB的中点，R为SC的中点，所以QR∥BC且QR＝BC.
所以QR∥PD且QR＝PD，则四边形PDRQ为平行四边形，所以PQ∥DR.
又PQ平面SCD，DR平面SCD，
所以PQ∥平面SCD.
【解析】：
分析：（Ⅰ）证明CD⊥AD，然后证明CD⊥平面SAD．
（Ⅱ）取SC的中点R，连QR，DR．推出PD=
BC，QR∥BC且QR=BC．然后证明四边形PDRQ为平行四边形，即可证明PQ∥平面SCD．
详解：
(1)因为四边形ABCD为正方形，所以CD⊥AD.
又平面SAD⊥平面ABCD，且平面SAD∩平面ABCD＝AD，
所以CD⊥平面SAD.
(2)取SC的中点R，连接QR，DR.
由题意知，PD∥BC且PD＝BC.
在△SBC中，Q为SB的中点，R为SC的中点，所以QR∥BC且QR＝BC.
所以QR∥PD且QR＝PD，则四边形PDRQ为平行四边形，所以PQ∥DR.
又PQ平面SCD，DR平面SCD，
所以PQ∥平面SCD.
练习册系列答案
相关题目
