题目内容
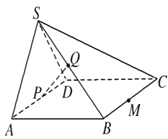
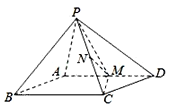
【题目】如图,已知四棱锥P-ABCD的底面ABCD是平行四边形,PA⊥平面ABCD.M是AD的中点,N是PC的中点.
(1)求证:MN∥平面PAB;
(2)若平面PMC⊥平面PAD,求证:CM⊥AD;
(3)若平面ABCD是矩形,PA=AB,求证:平面PMC⊥平面PBC.
【答案】(1)见解析(2)见解析(3)见解析
【解析】
(1)取PB的中点E,连接EN,AE,证明MN∥AE,即证MN∥平面PAB;(2)假设CM与AD不垂直,在平面ABCD内过M作AD的垂线,交BC于Q,连接PQ,MQ,证明平面PMQ⊥平面PAD,显然这与平面PMC⊥平面PAD矛盾.故原题得证;(3)先证明MN⊥平面PBC,即证平面PMC⊥平面PBC.
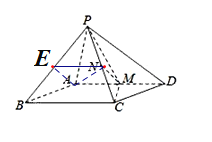
证明:(1)取PB的中点E,连接EN,AE.
∵E,N分别是PB,PC的中点,∴EN![]() BC,EN
BC,EN![]() BC,
BC,
∵M是AD的中点,四边形ABCD是平行四边形,
∴AM![]() BC ,AM
BC ,AM![]() BC,
BC,
∴EN![]() AM,EN
AM,EN![]() AM,∴四边形AMNE是平行四边形,
AM,∴四边形AMNE是平行四边形,
∴MN∥AE,
又MN平面PAB,AE平面PAB,
∴MN∥平面PAB.
(2)假设CM与AD不垂直,在平面ABCD内过M作AD的垂线,交BC于Q,连接PQ,MQ,

∵PA⊥平面ABCD,MQ平面ABCD,
∴PA⊥MQ,又AD⊥MQ,PA∩AD=A,
∴MQ⊥平面PAD,又MQ平面PMQ,
∴平面PMQ⊥平面PAD,
显然这与平面PMC⊥平面PAD矛盾.
故假设不成立,∴CM⊥AD.
(3)∵四边形ABCD是矩形,∴AD⊥AB,
∵PA⊥平面ABCD,AD平面ABCD,
∴PA⊥AD,又PA∩AB=A,
∴AD⊥平面PAB,∴AD⊥AE,
由(1)可知四边形AMNE是平行四边形,
∴四边形AMNE是矩形,
∴MN⊥EN,
又AM=MD,PA=AB=CD,∠PAM=∠MDC=90°,
∴△PMA≌△CMD,
∴PM=CM,又N是PC的中点,
∴MN⊥PC,
又PC∩EN=N,PC平面PBC,EN平面PBC,
∴MN⊥平面PBC,又MN平面PMC,
∴平面PMC⊥平面PBC.

【题目】在下列向量组中,可以把向量![]() =(3,2)表示出来的是( )
=(3,2)表示出来的是( )
A.![]() =(0,0),
=(0,0),![]() =(1,2)
=(1,2)
B.![]() =(﹣1,2),
=(﹣1,2),![]() =(5,﹣2)
=(5,﹣2)
C.![]() =(3,5),
=(3,5),![]() =(6,10)
=(6,10)
D.![]() =(2,﹣3),
=(2,﹣3), ![]() =(﹣2,3)
=(﹣2,3)
【题目】2017年5月14日,第一届“一带一路”国际高峰论坛在北京举行,为了解不同年龄的人对“一带一路”关注程度,某机构随机抽取了年龄在15-75岁之间的100人进行调查, 经统计“青少年”与“中老年”的人数之比为9:11
关注 | 不关注 | 合计 | |
青少年 | 15 | ||
中老年 | |||
合计 | 50 | 50 | 100 |
(1)根据已知条件完成上面的![]() 列联表,并判断能否有
列联表,并判断能否有![]() 的把握认为关注“一带一路”是否和年龄段有关?
的把握认为关注“一带一路”是否和年龄段有关?
(2)现从抽取的青少年中采用分层抽样的办法选取9人进行问卷调查.在这9人中再选取3人进行面对面询问,记选取的3人中关注“一带一路”的人数为X,求X的分布列及数学期望.
附:参考公式 ,其中
,其中![]()
临界值表:
| 0.05 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
【题目】某校高三年级一次数学考试后,为了解学生的数学学习情况,随机抽取![]() 名学生的数学成绩,制成表所示的频率分布表.
名学生的数学成绩,制成表所示的频率分布表.
组号 | 分组 | 频数 | 频率 |
第一组 |
|
|
|
第二组 |
|
|
|
第三组 |
|
|
|
第四组 |
|
|
|
第五组 |
|
|
|
合计 |
|
| |
(1)求![]() 、
、![]() 、
、![]() 的值;
的值;
(2)若从第三、四、五组中用分层抽样方法抽取![]() 名学生,并在这
名学生,并在这![]() 名学生中随机抽取
名学生中随机抽取![]() 名学生与张老师面谈,求第三组中至少有
名学生与张老师面谈,求第三组中至少有![]() 名学生与张老师面谈的概率
名学生与张老师面谈的概率