题目内容
7.在△ABC中角A,B,C的对边分别是a,b,c,且bsinA=$\sqrt{3}$cosB.(Ⅰ)求角B的大小;
(Ⅱ)若a=4,c=3,D为BC的中点,求AD的长度.
分析 (Ⅰ)由正弦定理化简已知可得:sinBsinA=$\sqrt{3}$sinAcosB,由sinA≠0,解得tanB=$\sqrt{3}$,又B为三角形的内角,即可解得B的值.
(Ⅱ)由D为BC的中点,可得BD=2,在△ABD中,利用余弦定理即可解得AD的值.
解答 解:(Ⅰ)∵bsinA=$\sqrt{3}$cosB.
∴由正弦定理可得:sinBsinA=$\sqrt{3}$sinAcosB,
∵sinA≠0,
∴sinB=$\sqrt{3}$cosB,即tanB=$\sqrt{3}$,
∵B为三角形的内角,
∴B=60°…5分
(Ⅱ)∵a=4,c=3,
∵D为BC的中点,
∴BD=2,
∴在△ABD中,利用余弦定理可得:AD2=AB2+BD2-2AB•BDcosB=${3}^{2}+{2}^{2}-2×3×2×\frac{1}{2}$=7.
∴AD=$\sqrt{7}$…10分
点评 本题主要考查了正弦定理,余弦定理的综合应用,属于基本知识的考查.

练习册系列答案
 优等生题库系列答案
优等生题库系列答案 53天天练系列答案
53天天练系列答案
相关题目
17.已知函数f(x)=ln(x+1)+2x-m(m∈R)的一个零点附近的函数值的参考数据如表:
由二分法,方程ln(x+1)+2x-m=0的近似解(精确度0.05)可能是( )
| x | 0 | 0.5 | 0.53125 | 0.5625 | 0.625 | 0.75 | 1 |
| f(x) | -1.307 | -0.084 | -0.009 | 0.066 | 0.215 | 0.512 | 1.099 |
| A. | 0.625 | B. | -0.009 | C. | 0.5625 | D. | 0.066 |
15.正方体ABCD-A1B1C1D1的棱长为1,M是棱AB的中点,点P是平面ABCD上的动点,P到直线A1D1的距离为d,且d2-|PM|2=1,则动点P的轨迹是( )
| A. | 圆 | B. | 抛物线 | C. | 椭圆 | D. | 双曲线 |
2.已知向量$\overrightarrow{a}$=(k,3),$\overrightarrow{b}=(1,4)$,$\overrightarrow{c}$=(1,-3),且(2$\overrightarrow{a}-3\overrightarrow{b}$)$⊥(\overrightarrow{b}+\overrightarrow{c})$,则实数k=( )
| A. | -$\frac{9}{2}$ | B. | 0 | C. | 3 | D. | $\frac{15}{2}$ |
12.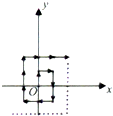 如图所示,质点A从坐标原点O开始沿箭头所指方向作规则运动,每次只运动一个单位,相应的质点的坐标记为An,如A1(0,1),A2(1,1),A3(1,0),A4(1,-1),…,则A2015的坐标为( )
如图所示,质点A从坐标原点O开始沿箭头所指方向作规则运动,每次只运动一个单位,相应的质点的坐标记为An,如A1(0,1),A2(1,1),A3(1,0),A4(1,-1),…,则A2015的坐标为( )
 如图所示,质点A从坐标原点O开始沿箭头所指方向作规则运动,每次只运动一个单位,相应的质点的坐标记为An,如A1(0,1),A2(1,1),A3(1,0),A4(1,-1),…,则A2015的坐标为( )
如图所示,质点A从坐标原点O开始沿箭头所指方向作规则运动,每次只运动一个单位,相应的质点的坐标记为An,如A1(0,1),A2(1,1),A3(1,0),A4(1,-1),…,则A2015的坐标为( )| A. | (-21,12) | B. | (-22,12) | C. | (-21,13) | D. | (-22,13) |