题目内容
数列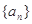 的前n项和记为
的前n项和记为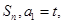 点
点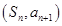 在直线
在直线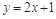 上,
上,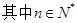 .(1)若数列
.(1)若数列 是等比数列,求实数
是等比数列,求实数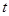 的值;
的值;
(2)设各项均不为0的数列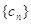 中,所有满足
中,所有满足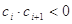 的整数
的整数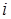 的个数称为这个数列
的个数称为这个数列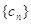 的“积异号数”,令
的“积异号数”,令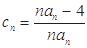 (
(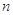
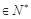 ),在(1)的条件下,求数列
),在(1)的条件下,求数列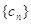 的“积异号数”
的“积异号数”
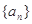 的前n项和记为
的前n项和记为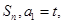 点
点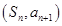 在直线
在直线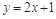 上,
上,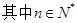 .(1)若数列
.(1)若数列 是等比数列,求实数
是等比数列,求实数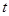 的值;
的值;(2)设各项均不为0的数列
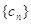 中,所有满足
中,所有满足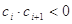 的整数
的整数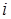 的个数称为这个数列
的个数称为这个数列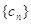 的“积异号数”,令
的“积异号数”,令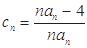 (
(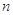
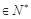 ),在(1)的条件下,求数列
),在(1)的条件下,求数列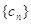 的“积异号数”
的“积异号数”(1)1 (2)1
试题分析:(1)根据数列的第n项与前n项和的关系可得n≥2时,有
 ,化简得an+1=3an(n≥2),要使n≥1时{an}是等比数列,只需
,化简得an+1=3an(n≥2),要使n≥1时{an}是等比数列,只需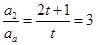 ,从而得出t的值.
,从而得出t的值.(2)由条件求得cn=1?
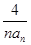 =
=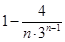 ,计算可得c1c2=-1<0,再由cn+1-cn>0可得,数列{cn}递增,由c2=
,计算可得c1c2=-1<0,再由cn+1-cn>0可得,数列{cn}递增,由c2=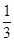 >0,得当n≥2时,cn>0,由此求得数列{cn}的“积异号数”为1.
>0,得当n≥2时,cn>0,由此求得数列{cn}的“积异号数”为1.(1)由题意,当
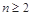 时,有
时,有
两式相减,得
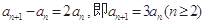 , 3分
, 3分所以,当
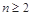 时
时 是等比数列,要使
是等比数列,要使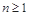 时
时 是等比数列,则只需
是等比数列,则只需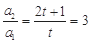
从而得出
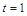 5分
5分(2)由(1)得,等比数列
 的首项为
的首项为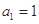 ,公比
,公比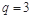 ,∴
,∴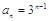
∴
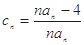
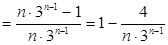 7分
7分∵
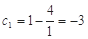 ,
,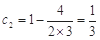 ,∴
,∴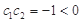
∵
 ,
,∴数列
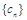 递增. 10分
递增. 10分由
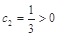 ,得当
,得当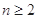 时,
时,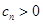 .
.∴数列
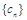 的“积异号数”为1. 12分
的“积异号数”为1. 12分
练习册系列答案
相关题目
 的前
的前 项和为
项和为 ,且满足
,且满足
 .
. ,
, ,
, ,
, 的值并写出其通项公式;(2)证明数列
的值并写出其通项公式;(2)证明数列 是公比大于1的等比数列,
是公比大于1的等比数列, 为数列
为数列 项和,已知
项和,已知 ,且
,且 构成等差数列.
构成等差数列. ,求数列
,求数列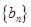 的前
的前 .
.
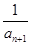 -
-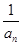 =d(n∈N*,d为常数),则称数列{an}为“调和数列”.已知正项数列{
=d(n∈N*,d为常数),则称数列{an}为“调和数列”.已知正项数列{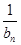 }为“调和数列”,且b1+b2+…+b9=90,则b4·b6的最大值是( )
}为“调和数列”,且b1+b2+…+b9=90,则b4·b6的最大值是( ) ,
, ,
, ,
, ,…为梯形数.根据图形的构成,记此数列的第
,…为梯形数.根据图形的构成,记此数列的第 项为
项为 ,则
,则 ( )
( )



