题目内容
设数列{an}的前n项和为Sn=10n-n2,则|a1|+|a2|+…+|a15|等于( )
| A.150 | B.135 | C.125 | D.100 |
根据an=
,得
当n≥2时,an=Sn-Sn-1=-n2+10n-[-(n-1)2+10(n-1)]=-2n+11,
当n=1时,S1=a1=9也适合上式,
∴an=-2n+11,
据通项公式得a1>a2>…>a5>0>a6>a7>…>a15
∴|a1|+|a2|+…+|a15|
=(a1+a2+…+a5)-(a6+a7+…+a15)
=2S5-S15
=2×(10×5-52)-(10×15-152)
=50+75
=125.
故选C.
|
当n≥2时,an=Sn-Sn-1=-n2+10n-[-(n-1)2+10(n-1)]=-2n+11,
当n=1时,S1=a1=9也适合上式,
∴an=-2n+11,
据通项公式得a1>a2>…>a5>0>a6>a7>…>a15
∴|a1|+|a2|+…+|a15|
=(a1+a2+…+a5)-(a6+a7+…+a15)
=2S5-S15
=2×(10×5-52)-(10×15-152)
=50+75
=125.
故选C.

练习册系列答案
 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案
相关题目
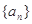 的前n项和记为
的前n项和记为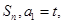 点
点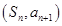 在直线
在直线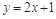 上,
上,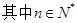 .(1)若数列
.(1)若数列 是等比数列,求实数
是等比数列,求实数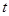 的值;
的值;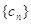 中,所有满足
中,所有满足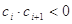 的整数
的整数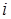 的个数称为这个数列
的个数称为这个数列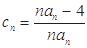 (
(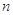
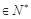 ),在(1)的条件下,求数列
),在(1)的条件下,求数列