题目内容
【题目】给定数列![]() ,若满足
,若满足![]() (
(![]() 且
且![]() ),对于任意的
),对于任意的![]() ,都有
,都有![]() ,则称数列
,则称数列![]() 为“指数型数列”.
为“指数型数列”.
(1)已知数列![]() 的通项公式为
的通项公式为![]() ,试判断数列
,试判断数列![]() 是不是“指数型数列”;
是不是“指数型数列”;
(2)已知数列![]() 满足
满足![]() ,
,![]() ,证明数列
,证明数列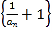 为等比数列,并判断数列
为等比数列,并判断数列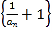 是否为“指数型数列”,若是给出证明,若不是说明理由;
是否为“指数型数列”,若是给出证明,若不是说明理由;
(3)若数列![]() 是“指数型数列”,且
是“指数型数列”,且![]() ,证明数列
,证明数列![]() 中任意三项都不能构成等差数列.
中任意三项都不能构成等差数列.
【答案】(1)是;(2)是,理由详见解析;(3)详见解析.
【解析】
(1)利用指数数列的定义,判断即可;
(2)利用a1![]() ,an=2anan+1+3an+1(n∈N*),说明数列{
,an=2anan+1+3an+1(n∈N*),说明数列{![]() 1}是等比数列,然后证明数列{
1}是等比数列,然后证明数列{![]() 1}为“指数型数列”;
1}为“指数型数列”;
(3)利用反证法,结合n为偶数以及奇数进行证明即可.
解:(1)数列![]() ,
,![]() ,所以数列
,所以数列![]() 是“指数型数列”
是“指数型数列”
(2)数列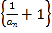 是“指数型数列”
是“指数型数列”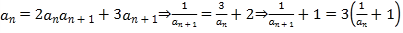 ,
,
所以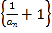 是等比数列,
是等比数列,
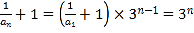 ,
,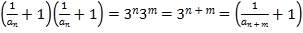
所以数列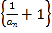 是“指数型数列”
是“指数型数列”
(3)若数列![]() 是“指数型数列”,由定义得:
是“指数型数列”,由定义得:
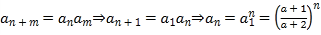
假设数列![]() 中存在三项
中存在三项![]() ,
,![]() ,
,![]() 成等差数列,不妨设
成等差数列,不妨设![]()
则![]() ,得:
,得: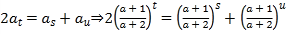
整理得:![]() (*)
(*)
若a为偶数时,右边为偶数,![]() 为奇数,则左边为奇数,(*)不成立;
为奇数,则左边为奇数,(*)不成立;
若a为奇数时,右边为偶数,![]() 为奇数,则左边为奇数,(*)不成立;
为奇数,则左边为奇数,(*)不成立;
所以,对任意的![]() ,(*)式不成立.
,(*)式不成立.

【题目】为了研究一种昆虫的产卵数![]() 和温度
和温度![]() 是否有关,现收集了7组观测数据列于下表中,并作出了如图的散点图.
是否有关,现收集了7组观测数据列于下表中,并作出了如图的散点图.
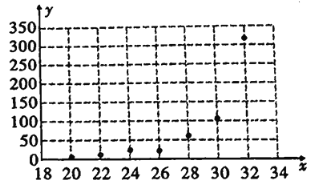
温度 | 20 | 22 | 24 | 26 | 28 | 30 | 32 |
产卵数 | 6 | 10 | 22 | 26 | 64 | 118 | 310 |
|
|
|
|
|
|
|
26 | 79.4 | 3.58 | 112 | 11.6 | 2340 | 35.72 |
其中![]() .
.
(1)根据散点图判断,![]() 与
与![]() 哪一个更适宜作为该昆虫的产卵数
哪一个更适宜作为该昆虫的产卵数![]() 与温度
与温度![]() 的回归方程类型?(给出判断即可,不必说明理由).
的回归方程类型?(给出判断即可,不必说明理由).
(2)根据表中数据,建立![]() 关于
关于![]() 的回归方程;(保留两位有效数字)
的回归方程;(保留两位有效数字)
(3)根据![]() 关于
关于![]() 的回归方程,估计温度为33℃时的产卵数.
的回归方程,估计温度为33℃时的产卵数.
(参考数据:![]() )
)
附:对于一组数据![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为
的斜率和截距的最小二乘估计分别为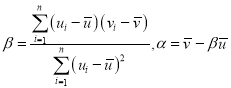 .
.