题目内容
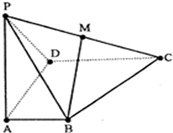 如图所示,四棱锥P-ABCD中,AB⊥AD,CD⊥AD,PA⊥底面ABCD,PA=AD=CD=2AB=2,M为PC的中点.
如图所示,四棱锥P-ABCD中,AB⊥AD,CD⊥AD,PA⊥底面ABCD,PA=AD=CD=2AB=2,M为PC的中点.(1)求证:BM∥平面PAD;
(2)在侧面PAD内找一点N,使MN⊥平面PBD;
(3)求直线PC与平面PBD所成角的正弦.
分析:(1)取PD的中点E,连接EM,EA,证明四边形ABME为平行四边形,可得BM∥AE,利用线面平行的判定,可证BM∥平面PAD;
(2)以A为原点,AB,AD,AP分别为x,y,z轴,建立空间直角坐标系,用坐标表示点与向量,利用
•
=0,
•
=0,即可确定N的坐标;
(3)设直线PC与平面PBD所成的角为θ,则
=(2,2,-2),
=(-1,-
,-
),利用向量的夹角公式,可求直线PC与平面PBD所成角的正弦值•
(2)以A为原点,AB,AD,AP分别为x,y,z轴,建立空间直角坐标系,用坐标表示点与向量,利用
| MN |
| PB |
| MN |
| DB |
(3)设直线PC与平面PBD所成的角为θ,则
| PC |
| MN |
| 1 |
| 2 |
| 1 |
| 2 |
解答:(1)证明:取PD的中点E,连接EM,EA,则EM∥AB,且EM=AB
所以四边形ABME为平行四边形,所以BM∥AE
又AE?平面PAD,BM不在平面PAD内,∴BM∥平面PAD;
(2)解:以A为原点,AB,AD,AP分别为x,y,z轴,建立空间直角坐标系
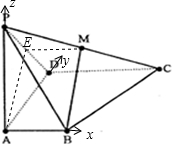
则B(1,0,0),C(2,2,0),D(0,2,0),P(0,0,2),M(1,1,1),E(0,1,1)
假设存在满足题意的点,则在平面PAD内,设N(0,y,z)
∴
=(-1,y-1,z-1),
=(1,0,-2),
=(1,-2,0)
由
•
=0,
•
=0,可得
,∴
∴N(0,
,
),∴N是AE的中点,此时MN⊥平面PBD;
(3)解:设直线PC与平面PBD所成的角为θ,则
=(2,2,-2),
=(-1,-
,-
),
设<
,
>为α,则cos<
,
>=
=
=-
∴sinθ=-cosα=
故直线PC与平面PBD所成角的正弦值为
•
所以四边形ABME为平行四边形,所以BM∥AE
又AE?平面PAD,BM不在平面PAD内,∴BM∥平面PAD;
(2)解:以A为原点,AB,AD,AP分别为x,y,z轴,建立空间直角坐标系

则B(1,0,0),C(2,2,0),D(0,2,0),P(0,0,2),M(1,1,1),E(0,1,1)
假设存在满足题意的点,则在平面PAD内,设N(0,y,z)
∴
| MN |
| PB |
| DB |
由
| MN |
| PB |
| MN |
| DB |
|
|
∴N(0,
| 1 |
| 2 |
| 1 |
| 2 |
(3)解:设直线PC与平面PBD所成的角为θ,则
| PC |
| MN |
| 1 |
| 2 |
| 1 |
| 2 |
设<
| PC |
| MN |
| PC |
| MN |
| ||||
|
|
| -2 | ||||||
2
|
| ||
| 3 |
∴sinθ=-cosα=
| ||
| 3 |
故直线PC与平面PBD所成角的正弦值为
| ||
| 3 |
点评:本题考查线面平行,考查线面垂直,考查线面角,考查利用空间向量解决立体几何问题,正确确定向量坐标是关键.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
 如图所示,四棱锥P-ABCD的底面为直角梯形,∠ADC=∠DCB=90°,AD=1,BC=3,PC=CD=2,PC⊥底面ABCD,E为AB的中点.
如图所示,四棱锥P-ABCD的底面为直角梯形,∠ADC=∠DCB=90°,AD=1,BC=3,PC=CD=2,PC⊥底面ABCD,E为AB的中点.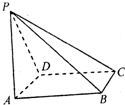 如图所示,四棱锥P-ABCD的底面是一个矩形,AB=3.AD=1.又PA⊥AB,PA=4,
如图所示,四棱锥P-ABCD的底面是一个矩形,AB=3.AD=1.又PA⊥AB,PA=4,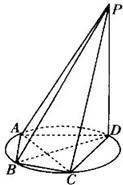 如图所示,四棱锥P-ABCD的底面ABCD是半径为R的圆的内接四边形,其中BD是圆的直径,∠ABD=60°,∠BDC=45°,△ADP~△BAD.
如图所示,四棱锥P-ABCD的底面ABCD是半径为R的圆的内接四边形,其中BD是圆的直径,∠ABD=60°,∠BDC=45°,△ADP~△BAD. (2012•烟台一模)如图所示,四棱锥P-ABCD中,ABCD为正方形,PA⊥AD,E,F,G分别是线段PA,PD,CD的中点.
(2012•烟台一模)如图所示,四棱锥P-ABCD中,ABCD为正方形,PA⊥AD,E,F,G分别是线段PA,PD,CD的中点. 如图所示,四棱锥P-ABCD底面是直角梯形,BA⊥AD,CD⊥AD,CD=2AB,PA⊥底面ABCD,E为PC的中点,PA=AD=AB=1.
如图所示,四棱锥P-ABCD底面是直角梯形,BA⊥AD,CD⊥AD,CD=2AB,PA⊥底面ABCD,E为PC的中点,PA=AD=AB=1.