题目内容
14.已知函数f(x)=x2+$\frac{54}{x}$,若函数y=f(x)-f(a)有三个零点,则实数a的取值范围(-∞,-6)∪(0,3)∪(3,+∞).分析 求导f′(x)=2x-$\frac{54}{{x}^{2}}$=$\frac{2x(x-3)({x}^{2}+3x+9)}{{x}^{2}}$,从而确定函数的单调性及最值,从而结合图象解出实数a的取值范围.
解答 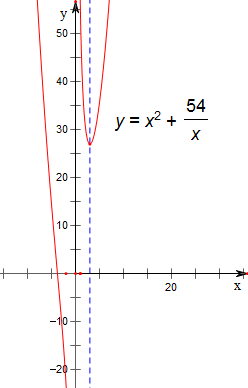 解:∵f(x)=x2+$\frac{54}{x}$,
解:∵f(x)=x2+$\frac{54}{x}$,
∴f′(x)=2x-$\frac{54}{{x}^{2}}$=$\frac{2x(x-3)({x}^{2}+3x+9)}{{x}^{2}}$,
∴当x∈(-∞,0)时,f′(x)<0,
当x∈(0,3)时,f′(x)<0,
当x∈(3,+∞)时,f′(x)>0,
∴f(x)在(-∞,0)上单调递减,
在(0,3)上单调递减,在(3,+∞)上单调递增;
f(3)=9+18=27,
故f(a)=a2+$\frac{54}{a}$>18=f(3),
即$\frac{(a+6)(a-3)^{2}}{a}$>0,
解得,a<-6或0<a<3或3<a,
故答案为:(-∞,-6)∪(0,3)∪(3,+∞).
点评 本题考查了导数的综合应用及数形结合的思想应用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
5.已知点(3,-2)是椭圆$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)上的点,则下列各点中,一定不在该椭圆上的是( )
| A. | (3,2) | B. | (-3,2) | C. | (-3,-2) | D. | (-2,3) |
6.在Rt△ABC中,CD是斜边上的高线,AC:BC=3:1,则S△ABC:S△BCD为( )
| A. | 4:3 | B. | 9:1 | C. | 10:1 | D. | 10:9 |
3.满足(n2-n-1)n+2=1的整数n有几个( )
| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
4.双曲线x2-2y2=2的渐近线方程为( )
| A. | y=±$\frac{\sqrt{2}}{2}$x | B. | y=±$\sqrt{2}$x | C. | y=±$\frac{1}{2}$x | D. | y=±2x |