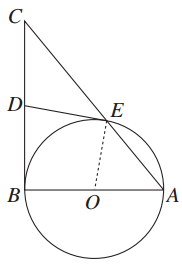
题目内容
已知圆 的方程为
的方程为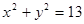 ,直线
,直线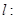
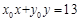 ,设点
,设点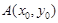 .
.
(1)若点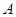 在圆
在圆 外,试判断直线
外,试判断直线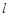 与圆
与圆 的位置关系;
的位置关系;
(2)若点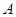 在圆
在圆 上,且
上,且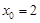 ,
,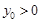 ,过点
,过点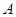 作直线
作直线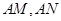 分别交圆
分别交圆 于
于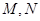 两点,且直线
两点,且直线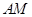 和
和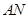 的斜率互为相反数;
的斜率互为相反数;
① 若直线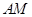 过点
过点 ,求
,求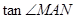 的值;
的值;
② 试问:不论直线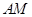 的斜率怎样变化,直线
的斜率怎样变化,直线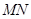 的斜率是否为定值?若是,求出该定值;若不是,说明理由.
的斜率是否为定值?若是,求出该定值;若不是,说明理由.
 的方程为
的方程为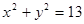 ,直线
,直线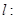
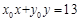 ,设点
,设点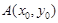 .
.(1)若点
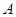 在圆
在圆 外,试判断直线
外,试判断直线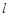 与圆
与圆 的位置关系;
的位置关系;(2)若点
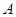 在圆
在圆 上,且
上,且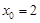 ,
,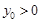 ,过点
,过点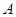 作直线
作直线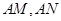 分别交圆
分别交圆 于
于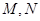 两点,且直线
两点,且直线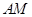 和
和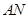 的斜率互为相反数;
的斜率互为相反数; ① 若直线
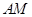 过点
过点 ,求
,求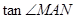 的值;
的值;② 试问:不论直线
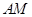 的斜率怎样变化,直线
的斜率怎样变化,直线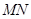 的斜率是否为定值?若是,求出该定值;若不是,说明理由.
的斜率是否为定值?若是,求出该定值;若不是,说明理由.(1)直线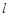 与圆
与圆 相交;
相交;
(2)①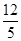 ;②不论直线
;②不论直线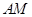 的斜率怎样变化,直线
的斜率怎样变化,直线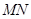 的斜率总为定值
的斜率总为定值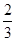
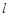 与圆
与圆 相交;
相交;(2)①
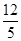 ;②不论直线
;②不论直线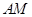 的斜率怎样变化,直线
的斜率怎样变化,直线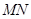 的斜率总为定值
的斜率总为定值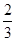
试题分析:(1)先由点A在园外得出
 ,再利用点到直线距离公式求出圆O圆心O到直线
,再利用点到直线距离公式求出圆O圆心O到直线 的距离与半径比较即可判定出直线
的距离与半径比较即可判定出直线 与圆O的位置关系;(2)①由直线斜率公式求出直线AM的斜率,再由直线
与圆O的位置关系;(2)①由直线斜率公式求出直线AM的斜率,再由直线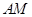 和
和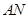 的斜率互为相反数,知直线
的斜率互为相反数,知直线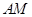 和
和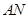 的倾斜角互补,将角AMN用直线AM的倾斜角表示出来,利用诱导公式及二倍角公式即可求出
的倾斜角互补,将角AMN用直线AM的倾斜角表示出来,利用诱导公式及二倍角公式即可求出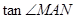 ;②设直线AM的斜率为k,写出直线AM方程,与圆O联立求出M点坐标,由题知AN的斜率为-k,同理求出M的坐标,利用斜率公式求出直线MN斜率,化简可知是否为定值.
;②设直线AM的斜率为k,写出直线AM方程,与圆O联立求出M点坐标,由题知AN的斜率为-k,同理求出M的坐标,利用斜率公式求出直线MN斜率,化简可知是否为定值.试题解析:(1)当点
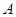 在圆
在圆 外时,得
外时,得 ,即
,即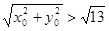
∴圆心到直线
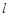 的距离
的距离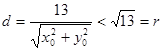 ,
,∴ 直线
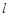 与圆
与圆 相交. 5分
相交. 5分(2)①由点
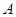 在圆
在圆 上,且
上,且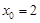 ,
,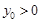 ,得
,得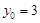 ,即
,即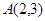 .
.记直线
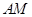 的倾斜角为
的倾斜角为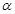 ,则
,则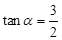 , 7分
, 7分又∵
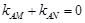 , ∴ 直线
, ∴ 直线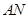 的倾斜角为
的倾斜角为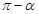 ,
,∴
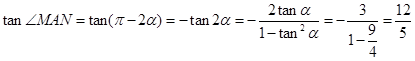 . 10分
. 10分②记直线
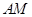 的斜率为
的斜率为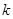 ,则直线
,则直线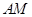 的方程为:
的方程为: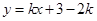 .
.将
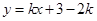 代入圆
代入圆 的方程得:
的方程得: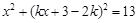 ,
,化简得:
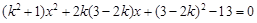 ,
,∵
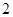 是方程的一个根, ∴
是方程的一个根, ∴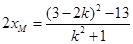 , ∴
, ∴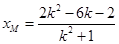 ,
,由题意知:
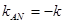 ,同理可得,
,同理可得,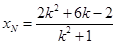 , 13分
, 13分∴
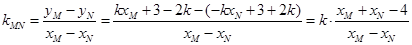 ,
,∴
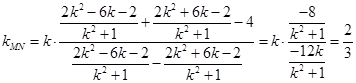 ,
,∴ 不论直线
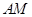 的斜率怎样变化,直线
的斜率怎样变化,直线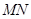 的斜率总为定值
的斜率总为定值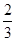 . 16分
. 16分
练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
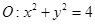 与坐标轴交于点
与坐标轴交于点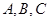 .
.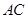 垂直的圆的切线方程;
垂直的圆的切线方程;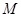 是圆上任意一点(不在坐标轴上),直线
是圆上任意一点(不在坐标轴上),直线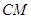 交
交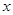 轴于点
轴于点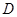 ,直线
,直线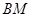 交直线
交直线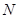 ,
,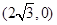 ,求弦
,求弦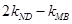 为定值.
为定值.
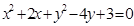 与直线
与直线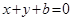 相切,正实数b的值为 ( )
相切,正实数b的值为 ( )
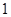
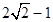
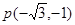 的直线l与圆
的直线l与圆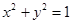 有公共点,则直线l的倾斜角的取值范围是
有公共点,则直线l的倾斜角的取值范围是




 :
: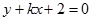 与曲线C:
与曲线C: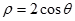 有交点,则
有交点,则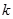 的取值范围是( )
的取值范围是( )