题目内容
已知两个点M(-3,0)和N(3,0),若直线上存在点P,使|PM|+|PN|=10,则称该直线为“A型直线”,则下列直线
①x=6②y=-5③y=x④y=2x+1中为“A型直线”的是______(填上所有正确结论的序号)
①x=6②y=-5③y=x④y=2x+1中为“A型直线”的是______(填上所有正确结论的序号)
已知两个点M(-3,0)和N(3,0),使|PM|+|PN|=10,
所以P的轨迹方程为:
+
=1.
画出椭圆与①x=6②y=-5③y=x④y=2x+1的图象.
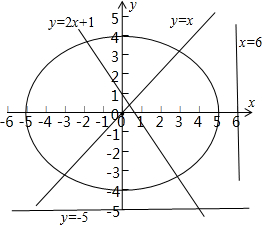
由图象可知,①x=6②y=-5与椭圆没有交点,不存在直线上存在点P,使|PM|+|PN|=10,
③y=x④y=2x+1与椭圆有交点,所以直线上存在点P,使|PM|+|PN|=10.
“A型直线”是③④.
故答案为:③④.
所以P的轨迹方程为:
| x2 |
| 25 |
| y2 |
| 16 |
画出椭圆与①x=6②y=-5③y=x④y=2x+1的图象.
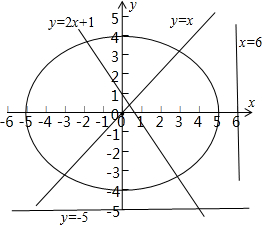
由图象可知,①x=6②y=-5与椭圆没有交点,不存在直线上存在点P,使|PM|+|PN|=10,
③y=x④y=2x+1与椭圆有交点,所以直线上存在点P,使|PM|+|PN|=10.
“A型直线”是③④.
故答案为:③④.

练习册系列答案
相关题目
 的圆
的圆 与
与 轴及直线
轴及直线 均相切,切点分别为
均相切,切点分别为 、
、 ,另一圆
,另一圆 与圆
与圆 、
、 。
。 的平行线
的平行线 ,求直线
,求直线
 的方程为
的方程为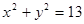 ,直线
,直线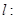
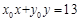 ,设点
,设点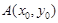 .
.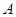 在圆
在圆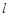 与圆
与圆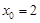 ,
,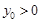 ,过点
,过点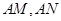 分别交圆
分别交圆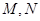 两点,且直线
两点,且直线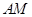 和
和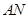 的斜率互为相反数;
的斜率互为相反数; 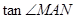 的值;
的值;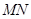 的斜率是否为定值?若是,求出该定值;若不是,说明理由.
的斜率是否为定值?若是,求出该定值;若不是,说明理由.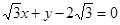 与圆
与圆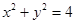 的位置关系是 (填相交、相切、相离)
的位置关系是 (填相交、相切、相离)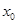 ,1),若在圆O:
,1),若在圆O: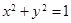 上存在点N,使得∠OMN=45°,则
上存在点N,使得∠OMN=45°,则