题目内容
过点P(1,2)作直线l与圆(x-2)2+y2=9相交于A,B两点,那么|AB|的最小值为( )
| A.2 | B.4 | C.3 | D.6 |
∵P(1,2)满足(1-2)2+22=5<9
∴点P是圆内的一点,
因此,当直线AB与CP互相垂直时,|AB|达到最小值(C为圆心(2,0))
∵|CP|=
=
∴直线AB与CP互相垂直时,|AB|=2
=2
=4
故选:B
∴点P是圆内的一点,
因此,当直线AB与CP互相垂直时,|AB|达到最小值(C为圆心(2,0))
∵|CP|=
| (1-2)2+(2-0)2 |
| 5 |
∴直线AB与CP互相垂直时,|AB|=2
| r2-|CP|2 |
| 9-5 |
故选:B

练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目
 的方程为
的方程为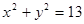 ,直线
,直线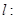
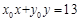 ,设点
,设点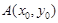 .
.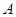 在圆
在圆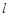 与圆
与圆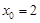 ,
,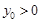 ,过点
,过点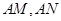 分别交圆
分别交圆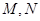 两点,且直线
两点,且直线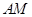 和
和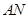 的斜率互为相反数;
的斜率互为相反数; 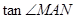 的值;
的值;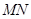 的斜率是否为定值?若是,求出该定值;若不是,说明理由.
的斜率是否为定值?若是,求出该定值;若不是,说明理由.