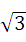题目内容
以Rt△ABC的直角边AB为直径的圆O交AC边于点E,点D在BC上,且DE与圆O相切.若∠A=56°,则∠BDE=________.
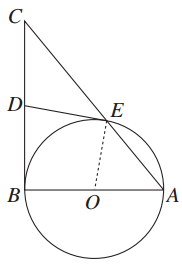

68°
如图所示,连接OE,则△OEA为等腰三角形,
∵OE=OA,∴∠OEA=∠A=56°,
∴∠EOA=68°,∵DE与圆O相切,且E在圆上.
∴OE⊥DE,即∠DEO=90°.
又∵∠B=90°,∴∠B+∠DEO=180°,
∴O、E、D、B四点共圆,∴∠BDE=∠EOA=68°.
∵OE=OA,∴∠OEA=∠A=56°,
∴∠EOA=68°,∵DE与圆O相切,且E在圆上.
∴OE⊥DE,即∠DEO=90°.
又∵∠B=90°,∴∠B+∠DEO=180°,
∴O、E、D、B四点共圆,∴∠BDE=∠EOA=68°.

练习册系列答案
相关题目
 的方程为
的方程为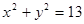 ,直线
,直线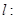
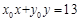 ,设点
,设点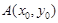 .
.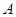 在圆
在圆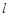 与圆
与圆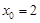 ,
,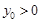 ,过点
,过点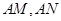 分别交圆
分别交圆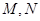 两点,且直线
两点,且直线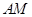 和
和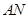 的斜率互为相反数;
的斜率互为相反数; 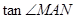 的值;
的值;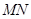 的斜率是否为定值?若是,求出该定值;若不是,说明理由.
的斜率是否为定值?若是,求出该定值;若不是,说明理由.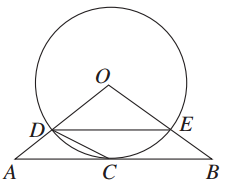
 ,求⊙O的半径r的长.
,求⊙O的半径r的长.
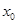 ,1),若在圆O:
,1),若在圆O: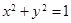 上存在点N,使得∠OMN=45°,则
上存在点N,使得∠OMN=45°,则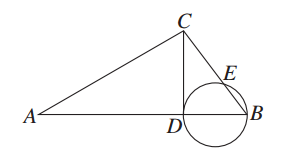
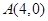 的直线
的直线 与曲线
与曲线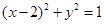 有公共点,则直线
有公共点,则直线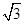 ,
,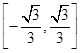
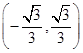
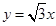 与圆
与圆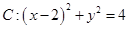 交于
交于 两点,则弦长
两点,则弦长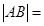 ( )
( )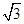
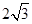
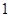
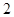
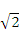 ,0)引直线ι与曲线
,0)引直线ι与曲线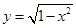 交于A,B两点 ,O为坐标原点,当△AOB的面积取最大值时,直线ι的斜率等于( )
交于A,B两点 ,O为坐标原点,当△AOB的面积取最大值时,直线ι的斜率等于( )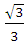 B.-
B.-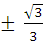 D-
D-