题目内容
| ∫ | 1 -1 |
(
|
| π |
| 2 |
| π |
| 2 |
分析:由于
,第一个积分根据积分所表示的几何意义是以(0,0)为圆心,1为半径第一、二象限内圆弧与坐标轴围成的面积,只需求出圆的面积乘以二分之一即可,第二个积分利用公式进行计算即可.
| ∫ | -1 1 |
(
|
| ∫ | 1 -1 |
(
|
| ∫ | 1 -1 |
|
解答:解:由于
,
dx表示的几何意义是:以(0,0)为圆心,1为半径第一,二象限内圆弧与坐标轴围成的面积
dx=
π×1=
,
又
xdx=
x2
=0,
∴原式=
+0=
.
故答案为:
.
| ∫ | 1 -1 |
(
|
| ∫ | 1 -1 |
|
| ∫ | 1 -1 |
| 1-x2 |
| ∫ | 1 -1 |
| 1-x2 |
| 1 |
| 2 |
| π |
| 2 |
又
| ∫ | 1 -1 |
| 1 |
| 2 |
| | | 1 -1 |
∴原式=
| π |
| 2 |
| π |
| 2 |
故答案为:
| π |
| 2 |
点评:本题主要考查了定积分,定积分运算是求导的逆运算,解题的关键是求原函数,也可利用几何意义进行求解,属于基础题.

练习册系列答案
相关题目
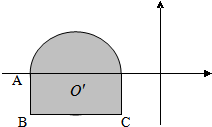 已知平面区域(含边界,上半部分为半圆,下半部分为矩形)如图,动点A(x,y)在该平面区域内,已知A(-3,0),C(-1,-1).
已知平面区域(含边界,上半部分为半圆,下半部分为矩形)如图,动点A(x,y)在该平面区域内,已知A(-3,0),C(-1,-1).