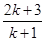题目内容
用数学归纳法证明"n∈N*时,x2n+1+a2n+1能被x+a整除" 的过程中.要证n＝k+1时命题成立, 代数式应变形到________才能得证.[ ]
A.x2k+3+a2k+3 B.x2．x2k+1+a2a2k+1
C.a2(x2k+1+a2k+1)-x2k+1(x2-a2) D.x2(x2k+1+a2k+1)-a2k+1(x2-a2)
答案：D
解析：
提示：
解析：
|
解: 当n＝k+1时 ∵ x2(k+1）+1+a2(k+1）+1 ＝x2k+3+a2k+3 ＝x2·x2k+1+a2·a2k+1 ＝x2(x2k+1+a2k+1)-x2·a2k+1+a2·a2k+1 ＝x2(x2k+1+a2k+1)-a2k+1(x2-a2) 又x2k+1+a2k+1和x2-a2均能被x+a整除 ∴ n＝k+1时命题成立. ∴ 选(D)
|
提示：
| 一定要用上归纳假设: x2k+1+a2k+1能被x+a整除. |
练习册系列答案
相关题目
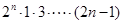(n∈N+)时，从“n=k到n=k+
B.
D.
+
+
+…+
≥
(n∈N*)”时，由“n=k到n=k+1”，不等式左边应添加的项是( )
+
+
-
+
-
-
(n∈N*)时，从n＝k到n＝k＋1，左端需要增加的代数式为（ ）
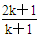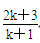
D．
D．. 