题目内容
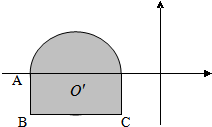 已知平面区域(含边界,上半部分为半圆,下半部分为矩形)如图,动点A(x,y)在该平面区域内,已知A(-3,0),C(-1,-1).
已知平面区域(含边界,上半部分为半圆,下半部分为矩形)如图,动点A(x,y)在该平面区域内,已知A(-3,0),C(-1,-1).(1)求x+y的最大值和最小值;
(2)求
| y | x-1 |
(3)求x2+y2-2x-2y+2的最大值和最小值.
分析:由图象分析,(1)x+y可转化为截距;(2)
表示斜率(3)x2+y2-2x-2y+2=(x-1)2+(y-1)2,表示可行域内的动点P(x,y)与定点N(1,1)距离的平方,结合图形易得其最值.
| y |
| x-1 |
解答: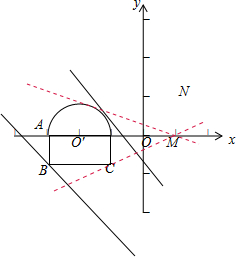 解:由题意结合图象
解:由题意结合图象
(1)设x+y=b,故y=-x+b,字母b为斜率为-1的直线的截距,由图可知:
当直线(黑色)过点B(-3,-1)时,截距最小,即x+y取最小值-3+(-1)=-4,
当直线与半圆相切时,截距最大,即x+y取最大值,
由直线和圆相切可得圆心O′(-2,0)到直线x+y=b的距离
=1,(圆的半径为1),
可解得b=-2+
,或b=-2-
(由图象可知不和题意,故舍去),
故求x+y的最大值和最小值分别为-2+
,-4;
(2)设k=
,则k表示可行域内动点P(x,y)与定点M(1,0)连线的斜率,…(5分)
由直线kx-y-k=0得,
=1得k=±
,知k≥-
,…(6分)
又kMC=
,…(7分)
故k∈[-
,
]; …(8分)
(3)设t=x2+y2-2x-2y+2=(x-1)2+(y-1)2,表示可行域内的动点P(x,y)与定点N(1,1)距离的平方,
由距离公式可得|NO′|=
=
,故tmin=(
-1)2=11-2
,
由图可知点B到N的距离最大,|NB|=
=
,故tmax=20 …(12分)
 解:由题意结合图象
解:由题意结合图象(1)设x+y=b,故y=-x+b,字母b为斜率为-1的直线的截距,由图可知:
当直线(黑色)过点B(-3,-1)时,截距最小,即x+y取最小值-3+(-1)=-4,
当直线与半圆相切时,截距最大,即x+y取最大值,
由直线和圆相切可得圆心O′(-2,0)到直线x+y=b的距离
| |-2-b| | ||
|
可解得b=-2+
| 2 |
| 2 |
故求x+y的最大值和最小值分别为-2+
| 2 |
(2)设k=
| y |
| x-1 |
由直线kx-y-k=0得,
| |3k| | ||
|
| ||
| 4 |
| ||
| 4 |
又kMC=
| 1 |
| 2 |
故k∈[-
| ||
| 4 |
| 1 |
| 2 |
(3)设t=x2+y2-2x-2y+2=(x-1)2+(y-1)2,表示可行域内的动点P(x,y)与定点N(1,1)距离的平方,
由距离公式可得|NO′|=
| (1+2)2+(1-0)2 |
| 10 |
| 10 |
| 10 |
由图可知点B到N的距离最大,|NB|=
| (1+3)2+(1+1)2 |
| 20 |
点评:本题考查线性规划问题,利用几何意义来求解是解决问题的关键,属中档题.

练习册系列答案
相关题目
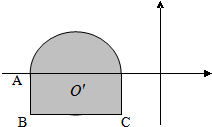 已知平面区域(含边界,上半部分为半圆,下半部分为矩形)如图,动点A(x,y)在该平面区域内,已知A(-3,0),C(-1,-1).
已知平面区域(含边界,上半部分为半圆,下半部分为矩形)如图,动点A(x,y)在该平面区域内,已知A(-3,0),C(-1,-1).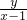 的取值范围;
的取值范围;