题目内容
(2013•天河区三模)设f(x)是定义在区间(1,+∞)上的函数,其导函数为f'(x).如果存在实数a和函数h(x),其中h(x)对任意的x∈(1,+∞)都有h(x)>0,使得f'(x)=h(x)(x2-ax+1),则称函数f(x)具有性质P(a).
(1)设函数f(x)=Inx+
(x>1),其中b为实数.
(i)求证:函数f(x)具有性质P(b);
(ii)求函数f(x)的单调区间.
(2)已知函数g(x)具有性质P(2),给定x1,x2∈(1,+∞),x1<x2,设m为实数,a=mx1+(1-m)x2,β=(1-m)x1+mx2,且a>1,β>1,若|g(a)-g(β)|<|g(x1)-g(x2)|,求m取值范围.
(1)设函数f(x)=Inx+
| b+2 | x+1 |
(i)求证:函数f(x)具有性质P(b);
(ii)求函数f(x)的单调区间.
(2)已知函数g(x)具有性质P(2),给定x1,x2∈(1,+∞),x1<x2,设m为实数,a=mx1+(1-m)x2,β=(1-m)x1+mx2,且a>1,β>1,若|g(a)-g(β)|<|g(x1)-g(x2)|,求m取值范围.
分析:(1)(i)先求出函数f(x)的导函数f′(x),然后将其配凑成f′(x)=h(x)(x2-bx+1)这种形式,再说明h(x)对任意的x∈(1,+∞)都有h(x)>0,即可证明函数f(x)具有性质P(b);
(2)根据第一问令φ(x)=x2-bx+1,讨论对称轴与2的大小,当b≤2时,对于x>1,φ(x)>0,所以f′(x)>0,可得f(x)在区间(1,+∞)上单调性,当b>2时,φ(x)图象开口向上,对称轴 x=
>1,可求出方程φ(x)=0的两根,判定两根的范围,从而确定φ(x)的符号,得到f′(x)的符号,最终求出单调区间.
(2)由题设知,函数g(x)得导数g′(x)=h(x)(x2-2x+1),其中h(x)>0对于任意得x∈(1,+∞)都成立
当x>1时,g′(x)=h(x)(x-1)2>0,从而g(x)在(1,+∞)上单调递增分①m∈(0,1)②m≤0③m≥1三种情况讨论求解m得范围即可
(2)根据第一问令φ(x)=x2-bx+1,讨论对称轴与2的大小,当b≤2时,对于x>1,φ(x)>0,所以f′(x)>0,可得f(x)在区间(1,+∞)上单调性,当b>2时,φ(x)图象开口向上,对称轴 x=
| b |
| 2 |
(2)由题设知,函数g(x)得导数g′(x)=h(x)(x2-2x+1),其中h(x)>0对于任意得x∈(1,+∞)都成立
当x>1时,g′(x)=h(x)(x-1)2>0,从而g(x)在(1,+∞)上单调递增分①m∈(0,1)②m≤0③m≥1三种情况讨论求解m得范围即可
解答:解:(1)f′(x)=
-
=
(x2-bx+1)
∵x>1时,h(x)=
>0恒成立,
∴函数f(x)具有性质P(b);
(ii)当b≤2时,对于x>1,φ(x)=x2-bx+1≥x2-2x+1=(x-1)2>0
所以f′(x)>0,故此时f(x)在区间(1,+∞)上递增;
当b>2时,φ(x)图象开口向上,对称轴 x=
>1,
方程φ(x)=0的两根为:
,
而
>1,
=
∈(0,1)
当 x∈(1,
)时,φ(x)<0,f′(x)<0,
故此时f(x)在区间 (1,
)上递减;
同理得:f(x)在区间[
,+∞)上递增.
综上所述,当b≤2时,f(x)在区间(1,+∞)上递增;
当b>2时,f(x)在 (1,,
)上递减;f(x)在[
,+∞)上递增.
(2)由题设知,函数g(x)得导数g′(x)=h(x)(x2-2x+1),其中h(x)>0对于任意得x∈(1,+∞)都成立
∴当x>1时,g′(x)=h(x)(x-1)2>0,从而g(x)在(1,+∞)上单调递增
①m∈(0,1),α=mx1+(1-m)x2>mx1+(1-m)x1=x1
α<mx2+(1-m)x2=x2
∴α∈(x1,x2)同理可得β∈(x1,x2)
由g(x)得单调性可知,g(α),g(β)∈(g(x1),g(x2))
从而有|g(α)-g(β)|≥|g(x1)-g(x2)|符合题意
②m≤0时,α=mx1+(1-m)x2≥mx2+(1-m)x2=x2
β=(1-m)x1+mx2≤(1-m)x1+mx1=mx1
于是由α>1,β>1及g(x)得单调性可知g(β)≤g(x1)<g(x2)≤g(α)
∴|g(α)-g(β)|≥|g(x1)-g(x2)|与题设不符
③m≥1时,同理可得α≤x1,β≥x2,进而可得|g(α)-g(β)|≥|g(x1)-g(x2)|与题设不符
综合①②③可得m∈(0,1)
| 1 |
| x |
| b+2 |
| (x+1)2 |
| 1 |
| x(x+1)2 |
∵x>1时,h(x)=
| 1 |
| x(x+1)2 |
∴函数f(x)具有性质P(b);
(ii)当b≤2时,对于x>1,φ(x)=x2-bx+1≥x2-2x+1=(x-1)2>0
所以f′(x)>0,故此时f(x)在区间(1,+∞)上递增;
当b>2时,φ(x)图象开口向上,对称轴 x=
| b |
| 2 |
方程φ(x)=0的两根为:
b+
| ||
| 2 |
b-
| ||
| 2 |
而
b+
| ||
| 2 |
b-
| ||
| 2 |
| 2 | ||
b+
|
当 x∈(1,
b+
| ||
| 2 |
故此时f(x)在区间 (1,
b+
| ||
| 2 |
同理得:f(x)在区间[
b+
| ||
| 2 |
综上所述,当b≤2时,f(x)在区间(1,+∞)上递增;
当b>2时,f(x)在 (1,,
b+
| ||
| 2 |
b+
| ||
| 2 |
(2)由题设知,函数g(x)得导数g′(x)=h(x)(x2-2x+1),其中h(x)>0对于任意得x∈(1,+∞)都成立
∴当x>1时,g′(x)=h(x)(x-1)2>0,从而g(x)在(1,+∞)上单调递增
①m∈(0,1),α=mx1+(1-m)x2>mx1+(1-m)x1=x1
α<mx2+(1-m)x2=x2
∴α∈(x1,x2)同理可得β∈(x1,x2)
由g(x)得单调性可知,g(α),g(β)∈(g(x1),g(x2))
从而有|g(α)-g(β)|≥|g(x1)-g(x2)|符合题意
②m≤0时,α=mx1+(1-m)x2≥mx2+(1-m)x2=x2
β=(1-m)x1+mx2≤(1-m)x1+mx1=mx1
于是由α>1,β>1及g(x)得单调性可知g(β)≤g(x1)<g(x2)≤g(α)
∴|g(α)-g(β)|≥|g(x1)-g(x2)|与题设不符
③m≥1时,同理可得α≤x1,β≥x2,进而可得|g(α)-g(β)|≥|g(x1)-g(x2)|与题设不符
综合①②③可得m∈(0,1)
点评:本题主要考查函数的概念、性质、图象及导数等基础知识,考查灵活运用数形结合、分类讨论的思想方法进行探索、分析与解决问题的综合能力.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
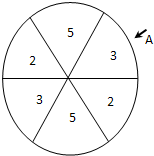 (2013•天河区三模)如图,一个圆形游戏转盘被分成6个均匀的扇形区域.用力旋转转盘,转盘停止转动时,箭头A所指区域的数字就是每次游戏所得的分数(箭头指向两个区域的边界时重新转动),且箭头A指向每个区域的可能性都是相等的.在一次家庭抽奖的活动中,要求每个家庭派一位儿童和一位成人先后分别转动一次游戏转盘,得分情况记为(a,b)(假设儿童和成人的得分互不影响,且每个家庭只能参加一次活动).
(2013•天河区三模)如图,一个圆形游戏转盘被分成6个均匀的扇形区域.用力旋转转盘,转盘停止转动时,箭头A所指区域的数字就是每次游戏所得的分数(箭头指向两个区域的边界时重新转动),且箭头A指向每个区域的可能性都是相等的.在一次家庭抽奖的活动中,要求每个家庭派一位儿童和一位成人先后分别转动一次游戏转盘,得分情况记为(a,b)(假设儿童和成人的得分互不影响,且每个家庭只能参加一次活动).