题目内容
已知f(x)=-2|2|x|-1|+1和g(x)=x2-2|x|+m(m∈R)是定义在R上的两个函数,则下列命题正确的是( )
分析:分析f(x)=-2|2|x|-1|+1和g(x)=x2-2|x|+m的函数性质,对选项逐个判断即可.
解答: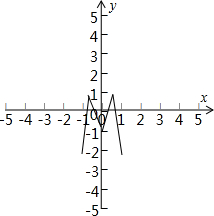 解:∵f(x)=-2|2|x|-1|+1,
解:∵f(x)=-2|2|x|-1|+1,
∴f(-x)=f(x),
∴f(x)=-2|2|x|-1|+1是偶函数,
x>0时,f(x)=-2|2x-1|+1=
,
∴f(x)=-2|2|x|-1|+1的图象如图所示,
∴关于x的方程f(x)-k=0恰有四个不相等实数根的充要条件是k∈(-1,1),即A不正确;
函数g(x)=x2-2|x|+m是偶函数,与y轴的交点坐标为(0,m),显然m=-
时,关于x的方程f(x)=g(x)有四个不相等实数根,故B不正确;
?x1∈[-1,0],f(x1)∈[-1,1],x2∈[-1,0],g(x)=x2+2x+1∈[0,1],
∴当m=1时,对?x1∈[-1,0],?x2∈[-1,0],f(x1)<g(x2)不成立,即C正确;
对于D,?x1∈[-1,1],?x2∈[-1,1],f(x1)≥g(x2)成立时,m≤-1,
∴若?x1∈[-1,1],?x2∈[-1,1],f(x1)<g(x2)成立,则m∈(-1,+∞),故D不正确.
故选D.
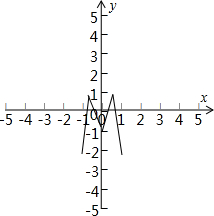 解:∵f(x)=-2|2|x|-1|+1,
解:∵f(x)=-2|2|x|-1|+1,∴f(-x)=f(x),
∴f(x)=-2|2|x|-1|+1是偶函数,
x>0时,f(x)=-2|2x-1|+1=
|
∴f(x)=-2|2|x|-1|+1的图象如图所示,
∴关于x的方程f(x)-k=0恰有四个不相等实数根的充要条件是k∈(-1,1),即A不正确;
函数g(x)=x2-2|x|+m是偶函数,与y轴的交点坐标为(0,m),显然m=-
| 1 |
| 2 |
?x1∈[-1,0],f(x1)∈[-1,1],x2∈[-1,0],g(x)=x2+2x+1∈[0,1],
∴当m=1时,对?x1∈[-1,0],?x2∈[-1,0],f(x1)<g(x2)不成立,即C正确;
对于D,?x1∈[-1,1],?x2∈[-1,1],f(x1)≥g(x2)成立时,m≤-1,
∴若?x1∈[-1,1],?x2∈[-1,1],f(x1)<g(x2)成立,则m∈(-1,+∞),故D不正确.
故选D.
点评:本题考查命题真假的判断,考查数形结合的数学思想,考查学生分析解决问题的能力,分析函数的性质是关键.

练习册系列答案
相关题目