题目内容
20．在△ABC中，D是AB边上的一点，若$\overrightarrow{CD}$=$\frac{1}{3}$$\overrightarrow{CA}$+$λ\overrightarrow{CB}$，则λ=$\frac{2}{3}$．分析 利用向量的基本定理结合向量的四则运算进行转化即可．
解答 解：如图：过作DE∥BC交AC于E，过D作DF∥AC，交BC于F，
∵$\overrightarrow{CD}$=$\frac{1}{3}$$\overrightarrow{CA}$+$λ\overrightarrow{CB}$，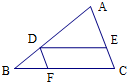
∴$\overrightarrow{CE}$=$\frac{1}{3}$$\overrightarrow{CA}$，从而$\overrightarrow{CD}$=$\frac{2}{3}\overrightarrow{CB}$=$λ\overrightarrow{CB}$，
解得λ=$\frac{2}{3}$，
故答案为：$\frac{2}{3}$
点评 本题主要考查向量的基本定理的应用，利用向量平行四边形法则是解决本题的关键．
练习册系列答案
能力评价系列答案
唐印文化课时测评系列答案
相关题目
10．焦点在x轴上的椭圆$\frac{{x}^{2}}{9}$+$\frac{{y}^{2}}{4+k}$=1的离心率为$\frac{4}{5}$，则k的值为（ ）
| A． | 21 | B． | $-\frac{181}{25}$ | C． | -$\frac{19}{25}$ | D． | $\frac{19}{25}$ |
11．若复数z=i3+$\frac{1}{1+i}$（i为虚数单位），则复数z的模为（ ）
| A． | 2$\sqrt{2}$ | B． | $\frac{{\sqrt{2}}}{2}$ | C． | $\frac{{\sqrt{10}}}{2}$ | D． | $\frac{{\sqrt{5}}}{2}$ |
15．已知x1，x2，…x9组成公差为1的等差数列，随机变量X所有取值为x1，x2，…x9，且等可能地取每一个值，则X的方差为（ ）
| A． | $\frac{20}{3}$ | B． | $\frac{10}{3}$ | C． | 60 | D． | 30 |
12．
如图，在梯形ABCD中，AD∥BC，$\overrightarrow{OA}$=$\overrightarrow a$，$\overrightarrow{OB}$=$\vec b$，$\overrightarrow{OC}$=$\overrightarrow c$，$\overrightarrow{OD}$=$\overrightarrow d$，且E、F分别为AB、CD的中点，则 （ ）
如图，在梯形ABCD中，AD∥BC，$\overrightarrow{OA}$=$\overrightarrow a$，$\overrightarrow{OB}$=$\vec b$，$\overrightarrow{OC}$=$\overrightarrow c$，$\overrightarrow{OD}$=$\overrightarrow d$，且E、F分别为AB、CD的中点，则 （ ）| A． | $\overrightarrow{EF}$=$\frac{1}{2}（\overrightarrow a+\overrightarrow b+\overrightarrow c+\overrightarrow d）$ | B． | $\overrightarrow{EF}$=$\frac{1}{2}（\overrightarrow a-\overrightarrow b+\overrightarrow c-\overrightarrow d）$ | C． | $\overrightarrow{EF}$=$\frac{1}{2}（-\overrightarrow a-\overrightarrow b+\overrightarrow c+\overrightarrow d）$ | D． | $\overrightarrow{EF}$=$\frac{1}{2}（\overrightarrow a+\overrightarrow b-\overrightarrow c-\overrightarrow d）$ |
9．在等差数列{an}中，Sn是其前n项和，a1=-2010，$\frac{{{S_{2008}}}}{2008}-\frac{{{S_{2006}}}}{2006}$=2，则S2010=（ ）
| A． | -2009 | B． | 2009 | C． | -2010 | D． | 2010 |