题目内容
设函数f(x)= 若f(m)<f(-m),则实数m的取值范围是
若f(m)<f(-m),则实数m的取值范围是
 若f(m)<f(-m),则实数m的取值范围是
若f(m)<f(-m),则实数m的取值范围是| A.(-1,0)∪(0,1) | B.(-∞,-1)∪(1,+∞) |
| C.(-1,0)∪(1,+∞) | D.(-∞,-1)∪(0,1) |
D
分析:分m大于0和m小于0两种情况考虑:当m大于0时,-m小于0,代入相应的解析式中求出f(m)和f(-m),将求出的解析式代入已知的不等式中,根据对数的运算性质及对数函数的单调性得到m的取值范围;当m小于0时,-m大于0,代入相应的解析式中求出f(m)和f(-m),将求出的解析式代入已知的不等式中,根据对数的运算性质及对数的单调性即可求出m的范围,综上,求出两个解集的并集即可得到实数m的取值范围.
解答:解:当m>0时,f(m)=log3m,f(-m)=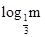 ,
,
代入不等式得:log3m<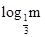 =-log3m,
=-log3m,
变形得:log3m<0=log31,
∵3>1,对数函数为递增函数,
∴0<m<1;
当m<0时,f(m)=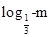 ,f(-m)=log3-m,
,f(-m)=log3-m,
代入不等式得: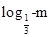 <log3-m,
<log3-m,
变形得:log3-m>0=log31,
∵3>1,对数函数为递增函数,
∴m<-1,
综上,实数m的取值范围为(-∞,-1)∪(0,1).
故选D.
解答:解:当m>0时,f(m)=log3m,f(-m)=
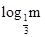 ,
,代入不等式得:log3m<
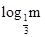 =-log3m,
=-log3m,变形得:log3m<0=log31,
∵3>1,对数函数为递增函数,
∴0<m<1;
当m<0时,f(m)=
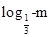 ,f(-m)=log3-m,
,f(-m)=log3-m,代入不等式得:
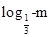 <log3-m,
<log3-m,变形得:log3-m>0=log31,
∵3>1,对数函数为递增函数,
∴m<-1,
综上,实数m的取值范围为(-∞,-1)∪(0,1).
故选D.

练习册系列答案
相关题目
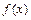 是以2为周期的周期函数,当
是以2为周期的周期函数,当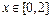 时,
时,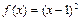 .
.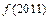 的值;
的值;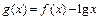 ,求函数
,求函数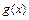 的零点的个数.
的零点的个数.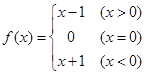 ,则
,则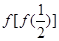 的值是
的值是 



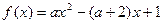 .若
.若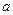 为整数,且函数
为整数,且函数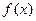 在
在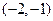 内恰有一个零点,求
内恰有一个零点,求
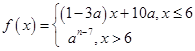 ,若数列
,若数列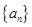 满足
满足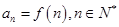 ,且
,且



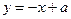 与曲线
与曲线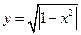 有三个交点,则
有三个交点,则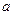 的取值范围是
的取值范围是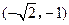
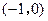
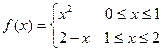 的图像与x轴所围成的封闭图形的面积为 。
的图像与x轴所围成的封闭图形的面积为 。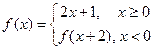 ,则
,则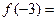 .
.