题目内容

9．0＜tanx＜1解集为{x|kπ＜x＜$\frac{π}{4}$+kπ，k∈Z}．

分析 根据正切函数的图象与性质，求出该不等式的解集即可．

解答 解：∵0＜tanx＜1，
∴kπ＜x＜$\frac{π}{4}$+kπ，k∈Z，
∴该不等式的解集为
{x|kπ＜x＜$\frac{π}{4}$+kπ，k∈Z}．
故答案为：{x|kπ＜x＜$\frac{π}{4}$+kπ，k∈Z}．

点评 本题考查了利用正切函数的图象与性质求不等式解集的应用问题，是基础题目．

练习册系列答案
相关题目
19．已知等比数列{an}中，a2=4，a5=32．
（1）求数列{an}的通项公式与前n项和Sn．
（2）设Tn=log2a1+log2a2+…+log2an，求Tn．
20．在△ABC中，a，b，c分别为角A，B，C所对的边，若a2＜b2-c2，则△ABC的形状为（　　）
A．锐角三角形B．直角三角形C．钝角三角形D．不能确定
17．在数列{an}中，a1=$\frac{1}{2}$，an+1=1-$\frac{1}{{a}_{n}}$，n∈N*，则a10=$\frac{1}{2}$．
4．已知椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1（a＞b＞0）$，设右焦点为F1，离心率为e．
（1）若椭圆过点$（\sqrt{2}，\sqrt{3}）$，$e=\frac{{\sqrt{2}}}{2}$，求椭圆的标准方程；
（2）若椭圆的焦距为4，设A、B为椭圆上关于原点对称的两点，且A、B在圆O：x2+y2=4上，设直线AB的斜率为k，若$k≥\sqrt{3}$，求e的取值范围．
14．已知等比数列{an}的前n项和为Sn，则下列一定成立的是（　　）
A．若a3＞0，则a2015＜0B．若a4＞0，则a2015＜0
C．若a3＞0，则a2015＞0D．若a4＞0，则a2015＞0
1．已知log53=a，5b=2，则5a+2b=12．
18．已知集合A={x|a-1≤x≤2a+3}，B={x|-2≤x≤4}，全集U=R．
（1）当a=2时，求A∩B和（∁RA）∩（∁RB）；
（2）若A∩B=A，求实数a的取值范围．
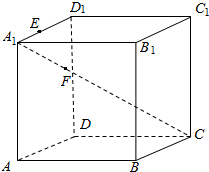19．如图所示，在正方体ABCD-A1B1C1D1中，E在A1D1上，且$\overrightarrow{{A}_{1}E}=2\overrightarrow{E{D}_{1}}$，F在对角线A1C上，且$\overrightarrow{{A}_{1}F}=\frac{2}{3}\overrightarrow{FC}$．求证：E，F，B三点共线．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网