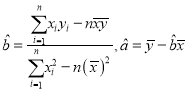题目内容
【题目】下列结论：
“直线l与平面
平行”是“直线l在平面外”的充分不必要条件；
若p：
，
，则
：
，
；
命题“设a，
，若
，则
或
”为真命题；
“
”是“函数
在
上单调递增”的充要条件．
其中所有正确结论的序号为______．
【答案】
【解析】
由线面的位置关系，结合充分必要条件的定义可判断
；由特称命题的否定为全称命题，可判断
；由原命题和逆否命题互为等价命题，可判断
；由导数大于等于0恒成立，结合充分必要条件的定义，可判断
．
“直线l与平面
平行”可推得“直线l在平面外”，反之，不成立，直线l可能与平面相交，故“直线l与平面平行”是“直线l在平面外”的充分不必要条件，故正确；
若p：
，
，则
：
，
，故错误；
命题“设a，
，若
，则
或
”的逆否命题为
“设a，，若
且
，则
”，即为真命题，故正确；
函数
在
上单调递增，可得
在恒成立，即有
的最小值，可得
，“
”是“函数在上单调递增”的充分不必要条件，故错误．
故答案为：．
练习册系列答案
相关题目
【题目】假设关于某设备的使用年限
和所支出的维修费用
（万元）有如下的统计资料：
使用年限 | 2 | 3 | 4 | 5 | 6 |
维修费用 | 2.2 | 3.8 | 5.5 | 6.5 | 7.0 |
若由资料知对呈线性相关关系．
（1）请画出上表数据的散点图；
（2）请根据最小二乘法求出线性回归方程
的回归系数
．
（3）估计使用年限为10年时，维修费用是多少？
