题目内容
15.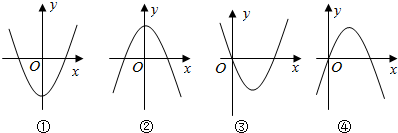 下面四个图象中,有一个是函数f(x)=$\frac{1}{3}$x3+ax2+(a2-1)x+1(a∈R)的导函数y=f′(x)的图象,则f(-1)=( )
下面四个图象中,有一个是函数f(x)=$\frac{1}{3}$x3+ax2+(a2-1)x+1(a∈R)的导函数y=f′(x)的图象,则f(-1)=( )| A. | $\frac{5}{3}$或$-\frac{1}{3}$ | B. | $\frac{5}{3}$或$\frac{1}{3}$ | C. | $-\frac{1}{3}$或$-\frac{5}{3}$ | D. | $\frac{1}{3}$或$-\frac{5}{3}$ |
分析 由f(x)解析式求出导函数f′(x)解析式,分析得到导函数图象可能为①或③,根据函数图象分别求出a的值,确定出f(x)解析式,即可求出f(-1)的值.
解答 解:由f(x)=$\frac{1}{3}$x3+ax2+(a2-1)x+1,得到f′(x)=x2+2ax+a2-1,
可得导函数图象可能为①,即对称轴为y轴,-a=0,
解得:a=0,此时f(x)=$\frac{1}{3}$x3-x+1,即f(-1)=-$\frac{1}{3}$+2=$\frac{5}{3}$;
可得导函数图象可能为③,即f′(0)=0,
∴a2-1=0,即a=1或-1,
当a=1时,f′(x)=x2+2x,不合题意;
当a=-1时,f(x)=$\frac{1}{3}$x3-x2+1,符合题意,此时f(-1)=-$\frac{1}{3}$-1+1=-$\frac{1}{3}$,
综上,f(-1)=$\frac{5}{3}$或-$\frac{1}{3}$,
故选:A.
点评 此题考查了导数的运算,二次函数的图象与性质,熟练掌握导数的运算是解本题的关键.

练习册系列答案
相关题目
7.已知集合A={x|-5<x<5},B={x|0<x≤7}.则A∪B=( )
| A. | (0,5) | B. | (-5,7) | C. | (-5,7] | D. | [-5,7) |
4.求函数y=lg(x2+x-6)的单调增区间是( )
| A. | $(-∞,-\frac{1}{2})$ | B. | $(-\frac{1}{2},+∞)$ | C. | (2,+∞) | D. | (-∞,-3) |
5.已知集合A={x|x>2},B={x|(x-1)(x-3)<0},则A∩B=( )
| A. | {x|x>1} | B. | {x|2<x<3} | C. | {x|1<x<3} | D. | {x|x>2或x<1} |
 如图所示,在四边形ABCD中,∠D=2∠B,且AD=2,CD=9,cosB=$\frac{1}{3}$.
如图所示,在四边形ABCD中,∠D=2∠B,且AD=2,CD=9,cosB=$\frac{1}{3}$.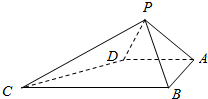 如图,四棱锥P-ABCD中,∠ABC=∠BAD=90°,BC=2AD,△PAB与△PAD都是边长为2的等边三角形.
如图,四棱锥P-ABCD中,∠ABC=∠BAD=90°,BC=2AD,△PAB与△PAD都是边长为2的等边三角形.