题目内容
关于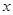 的方程
的方程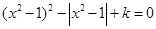 ,给出下列四个命题:
,给出下列四个命题:
①存在实数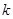 ,使得方程恰有2个不同实根; ②存在实数
,使得方程恰有2个不同实根; ②存在实数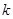 ,使得方程恰有4个不同实根;
,使得方程恰有4个不同实根;
③存在实数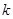 ,使得方程恰有5个不同实根; ④存在实数
,使得方程恰有5个不同实根; ④存在实数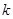 ,使得方程恰有8个不同实根;
,使得方程恰有8个不同实根;
其中假命题的个数是( )
| A.0 | B.1 | C.2 | D.3 |
A
解析试题分析:关于x的方程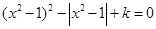 可化为
可化为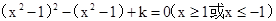 (1)
(1)
或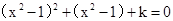 (-1<x<1)(2)
(-1<x<1)(2)
①当k=-2时,方程(1)的解为±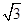 ,方程(2)无解,原方程恰有2个不同的实根;
,方程(2)无解,原方程恰有2个不同的实根;
②当k=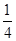 时,方程(1)有两个不同的实根±
时,方程(1)有两个不同的实根±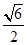 ,方程(2)有两个不同的实根±
,方程(2)有两个不同的实根±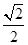 ,即原方程恰有4个不同的实根;
,即原方程恰有4个不同的实根;
③当k=0时,方程(1)的解为-1,+1,±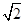 ,方程(2)的解为x=0,原方程恰有5个不同的实根;
,方程(2)的解为x=0,原方程恰有5个不同的实根;
④当k=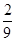 时,方程(1)的解为±
时,方程(1)的解为±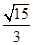 ,±
,±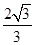 ,方程(2)的解为±
,方程(2)的解为±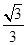 ,±
,±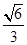 ,
,
即原方程恰有8个不同的实根.
∴四个命题都是真命题.故选A。
考点:本题主要考查函数方程思想,分类讨论思想。
点评:中档题,通过讨论x的范围,将方程中的绝对值符号去掉,这是一般思路。而k实施分类讨论又是基于函数值域。

练习册系列答案
 计算高手系列答案
计算高手系列答案
相关题目
设偶函数 的定义域为R,当
的定义域为R,当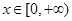 时,
时, 是增函数,则
是增函数,则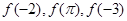 的大小关系是( )
的大小关系是( )
A.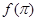 > >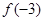 > >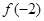 | B.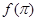 > >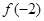 > >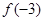 |
C.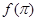 < <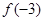 < <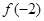 | D.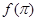 < <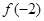 < <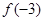 |
已知定义域为 的偶函数
的偶函数 在
在 上是减函数,且
上是减函数,且 ,则不等式
,则不等式 ( )
( )
A. | B. | C. | D. |
若存在实数x∈[2,4],使x2-2x+5-m<0成立,则m的取值范围为
| A.(13,+∞) | B.(5,+∞) | C.(4,+∞) | D.(-∞,13) |
已知函数 满足
满足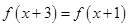 ,且
,且 ∈[-1,1]时,
∈[-1,1]时,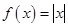 ,则函数
,则函数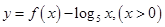 的零点个数是( )
的零点个数是( )
| A.3 | B.4 | C.5 | D.6 |
已知函数 中,常数
中,常数 那么
那么 的解集为
的解集为
A.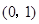 | B. | C. | D. |
下列函数中,在区间 上为减函数的是( )
上为减函数的是( )
A. | B. | C. | D. |
若a是函数 的零点,若
的零点,若 ,则
,则 的值满足
的值满足
A. | B. | C. | D. 的符号不确定 的符号不确定 |