题目内容
已知a,b,m,n,x,y都是正实数,且a<b,又知a,m,b,x成等差数列,a,n,b,y成等比数列,则有
- A.m>n,x>y
- B.m>n,x<y
- C.m<n,x>y
- D.m<n,x<y
B
分析:利用等差数列的定义及等比数列的定义得到m= ,
, ,利用基本不等式判断出m,n的大小;利用等差数列的定义得到b=
,利用基本不等式判断出m,n的大小;利用等差数列的定义得到b=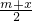 由均值不等式得
由均值不等式得 ,判断出x,y的大小.
,判断出x,y的大小.
解答:因为a,m,b,x成等差数列,a,n,b,y成等比数列,
m= ,
, ,
,
由基本不等式,
得m≥n
又a<b,
所以a,b,m,n,x,y互不相等,
所以m>n
b=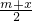 由均值不等式得
由均值不等式得
即 b>
b=
因为m>n
所以x<y
综上,得m>n,x<y,
故选B.
点评:本题考查等差数列及等比数列的性质,利用基本不等式比较数的大小,是一道中档题.
分析:利用等差数列的定义及等比数列的定义得到m=
 ,
, ,利用基本不等式判断出m,n的大小;利用等差数列的定义得到b=
,利用基本不等式判断出m,n的大小;利用等差数列的定义得到b=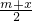 由均值不等式得
由均值不等式得 ,判断出x,y的大小.
,判断出x,y的大小.解答:因为a,m,b,x成等差数列,a,n,b,y成等比数列,
m=
 ,
, ,
,由基本不等式,
得m≥n
又a<b,
所以a,b,m,n,x,y互不相等,
所以m>n
b=
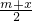 由均值不等式得
由均值不等式得
即 b>

b=

因为m>n
所以x<y
综上,得m>n,x<y,
故选B.
点评:本题考查等差数列及等比数列的性质,利用基本不等式比较数的大小,是一道中档题.

练习册系列答案
相关题目
已知a、b、m、n、x、y均为正数,且a≠b,若a、m、b、x成等差数列,a、n、b、y成等比数列,则有( )
| A、m>n,x>y | B、m>n,x<y | C、m<n,x<y | D、m<n,x>y |