题目内容
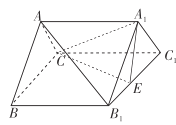
【题目】如图所示,四棱锥![]() 中,底面
中,底面![]() 为菱形,
为菱形,![]() 底面
底面![]() ,
,![]() ,
,![]() ,E为棱
,E为棱![]() 的中点,F为棱
的中点,F为棱![]() 上的动点.
上的动点.
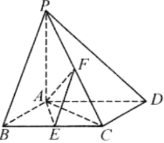
(1)求证:![]() 平面
平面![]() ;
;
(2)若锐二面角![]() 的正弦值为
的正弦值为![]() ,求点F的位置.
,求点F的位置.
【答案】(1)证明见解析(2)点F为线段![]() 的中点
的中点
【解析】
(1)证明![]() ,
,![]() 即可.
即可.
(2) 以点A为坐标原点,![]() 所在直线分别为
所在直线分别为![]() 轴建立空间直角坐标系
轴建立空间直角坐标系![]() ,设
,设![]() ,进而利用空间向量求解锐二面角
,进而利用空间向量求解锐二面角![]() 的正弦值关于
的正弦值关于![]() 的表达式,进而求得
的表达式,进而求得![]() 即可判断.
即可判断.
(1)如下图所示,由于四边形![]() 是菱形,则
是菱形,则![]() ,
,
又∵![]() ,∴
,∴![]() 是等边三角形,∵E为
是等边三角形,∵E为![]() 的中点,∴
的中点,∴![]() ,
,
∵![]() ,∴
,∴![]() .
.
∵![]() 底面
底面![]() ,
,![]() 平面
平面![]() ,∴
,∴![]() ,
,
∵![]() ,
,![]() 平面
平面![]() ,
,
∴![]() 平面
平面![]() ;
;
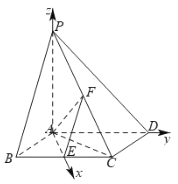
(2)由(1)知,![]() ,且
,且![]() 底面
底面![]() ,以点A为坐标原点,
,以点A为坐标原点,![]() 所在直线分别为
所在直线分别为![]() 轴建立空间直角坐标系
轴建立空间直角坐标系![]() ,
,
由![]() 则点,
则点,![]() ,
,
设![]() ,
,
则![]() ,
,
设平面![]() 的一个法向量为
的一个法向量为![]() ,
,
由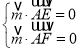 ,即
,即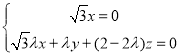 ,取
,取![]() ,则
,则![]() ,
,![]() ,则平面
,则平面![]() 的一个法向量为
的一个法向量为![]() ,
,
同理可得平面![]() 的一个法向量为
的一个法向量为![]() ,
,
∵二面角![]() 的正弦值为
的正弦值为![]()
∴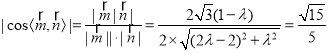 ,解得
,解得![]() .
.
因此,当点F为线段![]() 的中点时,二面角
的中点时,二面角![]() 的正弦值为
的正弦值为![]() .
.

 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案【题目】某人某天的工作是:驾车从![]() 地出发,到
地出发,到![]() 两地办事,最后返回
两地办事,最后返回![]() 地,
地,![]() 三地之间各路段行驶时间及当天降水概率如下表:
三地之间各路段行驶时间及当天降水概率如下表:
路段 | 正常行驶所需时间(小时) | 上午降水概率 | 下午降水概率 |
| 2 | 0.3 | 0.6 |
| 2 | 0.2 | 0.7 |
| 3 | 0.3 | 0.9 |
若在某路段遇到降水,则在该路段行驶的时间需延长1小时.
现有如下两个方案:
方案甲:上午从![]() 地出发到
地出发到![]() 地办事,然后到达
地办事,然后到达![]() 地, 下午在
地, 下午在![]() 地办事后返回
地办事后返回![]() 地;
地;
方案乙:上午从![]() 地出发到
地出发到![]() 地办事,下午从
地办事,下午从![]() 地出发到达
地出发到达![]() 地,办事后返回
地,办事后返回![]() 地.设此人8点从
地.设此人8点从![]() 地出发,在各地办事及午餐的累积时间为2小时.
地出发,在各地办事及午餐的累积时间为2小时.
现采用随机数表法获取随机数并进行随机模拟试验,按照以下随机数表,以方框内的数字5为起点,从左向右依次读取数据,若到达某行最后一个数字,则从下一行最左侧数字继续读取,每次读取4位随机数,第1位数表示采取的方案,其中0-4表示采用方案甲,5-9表示采用方案乙;第2-4位依次分别表示当天行驶的三个路段上是否降水,若某路段降水概率为![]() ,则
,则![]() 表示降水,
表示降水,![]() 表示不降水.(符号
表示不降水.(符号![]() 表示的数集包含
表示的数集包含![]() )
)
05 26 93 70 60 22 35 85 15 13 92 03 51 59 77 59 56 78 06 83 52 91 05 70 74
07 97 10 88 23099842 99 64 61 71 6299 15 06![]() 1 29 169358 05 77 05 91
1 29 169358 05 77 05 91
51 26 87 85 85 54 87 66 47 54 73 32 08 11 12 44 95 92 63 16 29 56 24 29 48
26 99 61 65 53 58 37 78 80 70 42 10 50 67 42 32 17 55 85 74 94 44 67 16 94
14 65 52 68 75 87 59 36 22 41 26 78 63 06 55 13 08 27 01 50 15 29 39 39 43
(1)利用数据“5129”模拟当天的情况,试推算他当日办完事返回![]() 地的时间;
地的时间;
(2)利用随机数表依次取出采用甲、乙方案的模拟结果各两组,分别计算甲、乙两个方案的平均时间,并回答哪个方案办完事后能尽早返回![]() 地.
地.