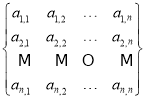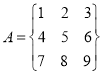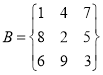题目内容
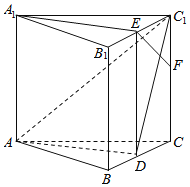
【题目】如图所示,在正三棱柱ABC-A1B1C1中,已知D,E分别为BC,B1C1的中点,点F在棱CC1上,且EF⊥C1D.求证:
(1)直线A1E∥平面ADC1;
(2)直线EF⊥平面ADC1.

【答案】(1)见解析;(2)见解析
【解析】
(1)先证明A1E∥AD,再证明直线A1E∥平面ADC1;(2)先证明AD⊥EF,EF⊥C1D,再证明直线EF⊥平面ADC1.
(1)连接ED,∵D,E分别为BC,B1C1的中点,
∴B1E∥BD且B1E=BD,
∴四边形B1BDE是平行四边形,
∴BB1∥DE且BB1=DE,又BB1∥AA1且BB1=AA1,
∴AA1∥DE且AA1=DE,
∴四边形AA1ED是平行四边形,
∴A1E∥AD,又∵A1E平面ADC1,AD平面ADC1,
∴直线A1E∥平面ADC1.
(2)在正三棱柱ABC-A1B1C1中,BB1⊥平面ABC,又AD平面ABC,所以AD⊥BB1,
又△ABC是正三角形,且D为BC的中点,
∴AD⊥BC,又BB1,BC平面B1BCC1,BB1∩BC=B,
∴AD⊥平面B1BCC1,又EF平面B1BCC1,
∴AD⊥EF,
又EF⊥C1D,C1D,AD平面ADC1,C1D∩AD=D,
∴直线EF⊥平面ADC1.

 备战中考寒假系列答案
备战中考寒假系列答案【题目】流行性感冒多由病毒引起,据调查,空气月平均相对湿度过大或过小时,都有利于一些病毒繁殖和传播,科学测定,当空气月平均相对湿度大于65010或小于![]() 时,有利于病毒繁殖和传播.下表记录了某年甲、乙两个城市12个月的空气月平均相对湿度.
时,有利于病毒繁殖和传播.下表记录了某年甲、乙两个城市12个月的空气月平均相对湿度.
第一季度 | 第二季度 | 第三季度 | 第四季度 | |||||||||
1月 | 2月 | 3月 | 4月 | 5月 | 6月 | 7月 | 8月 | 9月 | 10月 | 11月 | 12月 | |
甲地 |
|
|
|
|
|
|
|
|
|
|
| |
乙地 |
|
|
|
|
|
|
|
|
|
|
|
|
(I)从上表12个月中,随机取出1个月,求该月甲地空气月平均相对湿度有利于病毒繁殖和传播的概率;
(Ⅱ)从上表第一季度和第二季度的6个月中随机取出2个月,记这2个月中甲、乙两地空气月平均相对湿度都有利于病毒繁殖和传播的月份的个数为![]() ,求
,求![]() 的分布列;
的分布列;
(Ⅲ)若![]() ,设乙地上表12个月的空气月平均相对湿度的中位数为
,设乙地上表12个月的空气月平均相对湿度的中位数为![]() ,求
,求![]() 的最大值和最小值.(只需写出结论)
的最大值和最小值.(只需写出结论)