题目内容
【题目】习大大构建的“一带一路”经济带的发展规划已经得到了越来越多相关国家的重视和参与.某市顺潮流、乘东风,闻迅而动,决定利用旅游资源优势,撸起袖子大干一场.为了了解游客的情况,以便制定相应的策略.在某月中随机抽取甲、乙两个景点各10天的游客数,画出茎叶图如下: 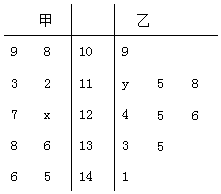
(1)若景点甲中的数据的中位数是125,景点乙中的数据的平均数是124,求x,y的值;
(2)若将图中景点甲中的数据作为该景点较长一段时期内的样本数据.今从这段时期中任取4天,记其中游客数超过120人的天数为ξ,求概率P(ξ≤2);
(3)现从上图的共20天的数据中任取2天的数据(甲、乙两景点中各取1天),记其中游客数不低于115且不高于125人的天数为η,求η的分布列和期望.
【答案】
(1)解:景点甲中的数据的中位数是125,可得X=3,景点乙中的数据的平均数是124,可得 ![]() =124,解得y=4;
=124,解得y=4;
(2)解:由题意知:因为景点甲的每一天的游客数超过120人的概率为 ![]() ,
,
任取4天,即是进行了4次独立重复试验,其中有ξ次发生,
故随机变量ξ服从二项分布,则P(ξ≤2)= ![]() ,
,
(3)解:从图中看出:景点甲的数据中符合条件的只有1天,景点乙的数据中符合条件的有4天.所以在景点甲中被选出的概率为 ![]() ,在景点乙中被选出的概率为
,在景点乙中被选出的概率为 ![]() .
.
由题意知:η的所有可能的取值为0,1,2.
则P(η=0)= ![]() P(η=1)=
P(η=1)= ![]() P(η=2)=
P(η=2)= ![]() ,
,
所以得分布列为:
η | 0 | 1 | 2 |
P | | | |
Е(η)=0× ![]() .
.
【解析】(1)利用景点甲中的数据的中位数是125,景点乙中的数据的平均数是124,直接求解x,y的值.(2)判断游客数超过120人的概率,判断是独立重复试验,满足二项分布,然后求解概率即可.(3)求出η的所有可能的取值为0,1,2,求出概率得到分布列,然后求解期望即可.
【考点精析】掌握茎叶图和离散型随机变量及其分布列是解答本题的根本,需要知道茎叶图又称“枝叶图”,它的思路是将数组中的数按位数进行比较,将数的大小基本不变或变化不大的位作为一个主干(茎),将变化大的位的数作为分枝(叶),列在主干的后面,这样就可以清楚地看到每个主干后面的几个数,每个数具体是多少;在射击、产品检验等例子中,对于随机变量X可能取的值,我们可以按一定次序一一列出,这样的随机变量叫做离散型随机变量.离散型随机变量的分布列:一般的,设离散型随机变量X可能取的值为x1,x2,.....,xi,......,xn,X取每一个值 xi(i=1,2,......)的概率P(ξ=xi)=Pi,则称表为离散型随机变量X 的概率分布,简称分布列.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】为了研究学生的数学核素养与抽象(能力指标x)、推理(能力指标y)、建模(能力指标z)的相关性,并将它们各自量化为1、2、3三个等级,再用综合指标w=x+y+z的值评定学生的数学核心素养;若w≥7,则数学核心素养为一级;若5≤w≤6,则数学核心素养为二级;若3≤w≤4,则数学核心素养为三级,为了了解某校学生的数学核素养,调查人员随机访问了某校10名学生,得到如下结果:
学生编号 | A1 | A2 | A3 | A4 | A5 | A6 | A7 | A8 | A9 | A10 |
(x,y,z) | (2,2,3) | (3,2,3) | (3,3,3) | (1,2,2) | (2,3,2) | (2,3,3) | (2,2,2) | (2,3,3) | (2,1,1) | (2,2,2) |
(1)在这10名学生中任取两人,求这两人的建模能力指标相同的概率;
(2)从数学核心素养等级是一级的学生中任取一人,其综合指标为a,从数学核心素养等级不是一级的学生中任取一人,其综合指标为b,记随机变量X=a﹣b,求随机变量X的分布列及其数学期望.