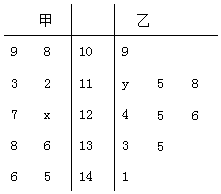
题目内容
【题目】如图,AB=BE=BC=2AD=2,且AB⊥BE,∠DAB=60°,AD∥BC,BE⊥AD,
(Ⅰ)求证:面ADE⊥面 BDE;
(Ⅱ)求直线AD与平面DCE所成角的正弦值..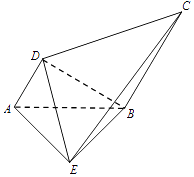
【答案】解:(Ⅰ)∵AB=2AD,∠DAB=60°,∴AD⊥DB,
又BE⊥AD,且BD∩BE=B,
∴AD⊥面BDE,又AD面ADE,∴面ADE⊥面 BDE;
(Ⅱ)∵BE⊥AD,AB⊥BE,∴BE⊥面ABCD,
∴点E到面ABCD的距离就是线段BE的长为2,
设AD与平面DCE所成角为θ,点A到面DCE的距离为d,
由VA﹣DCE=VE﹣ADC得: ![]() ,可解得
,可解得 ![]() ,
,
而AD=1,则 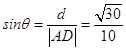 ,
,
故直线AD与平面DCE所成角的正弦值为 ![]() .
.
【解析】(Ⅰ)AB=2AD,∠DAB=60°,可得AD⊥DB,再利用线面面面垂直的判定与性质定理即可证明.(Ⅱ)由已知可得BE⊥面ABCD,点E到面ABCD的距离就是线段BE的长为2,设AD与平面DCE所成角为θ,点A到面DCE的距离为d,利用VA﹣DCE=VE﹣ADC,即可得出.
【考点精析】关于本题考查的平面与平面垂直的判定和空间角的异面直线所成的角,需要了解一个平面过另一个平面的垂线,则这两个平面垂直;已知![]() 为两异面直线,A,C与B,D分别是
为两异面直线,A,C与B,D分别是![]() 上的任意两点,
上的任意两点,![]() 所成的角为
所成的角为![]() ,则
,则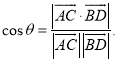 才能得出正确答案.
才能得出正确答案.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目