��Ŀ����
18����֪$\overrightarrow{a}$=��-3��2����$\overrightarrow{b}$=��-1��0����������$\overrightarrow{a}$+$\overrightarrow{b}$��$\overrightarrow{a}$-2$\overrightarrow{b}$��ֱ����ʵ���˵�ֵΪ��������| A�� | $\frac{1}{7}$ | B�� | -$\frac{1}{7}$ | C�� | $\frac{1}{6}$ | D�� | -$\frac{1}{6}$ |
���� ������������ֱ��������Ϊ0���г���������˵�ֵ���ɣ�
��� �⣺��$\overrightarrow{a}$=��-3��2����$\overrightarrow{b}$=��-1��0����
��${\overrightarrow{a}}^{2}$=13��${\overrightarrow{b}}^{2}$=1��$\overrightarrow{a}$•$\overrightarrow{b}$=3��
��������$\overrightarrow{a}$+$\overrightarrow{b}$��$\overrightarrow{a}$-2$\overrightarrow{b}$��ֱ��
�ࣨ��$\overrightarrow{a}$+$\overrightarrow{b}$��•��$\overrightarrow{a}$-2$\overrightarrow{b}$��=��${\overrightarrow{a}}^{2}$+��1-2�ˣ�$\overrightarrow{a}$•$\overrightarrow{b}$-2${\overrightarrow{b}}^{2}$=0��
��13��+3��1-2�ˣ�-2=0��
��æ�=-$\frac{1}{7}$��
��ѡ��B��
���� ���⿼����ƽ�������Ĵ�ֱ�������������⣬Ҳ������ƽ����������������Ӧ�����⣬�ǻ�����Ŀ��

��ϰ��ϵ�д�
�����Ŀ
13����cos��$\frac{��}{3}$-2x��=-$\frac{7}{8}$����cos��$\frac{��}{6}$-x����ֵΪ��������
| A�� | -$\frac{1}{4}$ | B�� | ��$\frac{1}{4}$ | C�� | $\frac{7}{8}$ | D�� | ��$\frac{7}{8}$ |
3����Բx2+y2-2kx+2y+2=0��k��0�����������������㣬��ôʵ��k��ȡֵ��Χ�ǣ�������
| A�� | 0��k��$\sqrt{2}$ | B�� | 1��k��$\sqrt{2}$ | C�� | 0��k��1 | D�� | k��$\sqrt{2}$ |
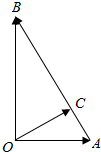 ��ͼ��ʾ����֪��B=30�㣬��A0B=90�㣬��C��AB�ϣ�0C��AB����$\overrightarrow{OA}��\overrightarrow{OB}$����ʾ����$\overrightarrow{OC}$����$\overrightarrow{OC}$����$\frac{3}{4}$$\overrightarrow{OA}$+$\frac{1}{4}$$\overrightarrow{OB}$��
��ͼ��ʾ����֪��B=30�㣬��A0B=90�㣬��C��AB�ϣ�0C��AB����$\overrightarrow{OA}��\overrightarrow{OB}$����ʾ����$\overrightarrow{OC}$����$\overrightarrow{OC}$����$\frac{3}{4}$$\overrightarrow{OA}$+$\frac{1}{4}$$\overrightarrow{OB}$��