题目内容
【题目】已知函数![]() 在
在![]() 处取得极值.
处取得极值.
![]() Ⅰ
Ⅰ![]() 求实数a的值;
求实数a的值;
![]() Ⅱ
Ⅱ![]() 若关于x的方程
若关于x的方程![]() 在
在![]() 上恰有两个不相等的实数根,求实数b的取值范围;
上恰有两个不相等的实数根,求实数b的取值范围;
![]() Ⅲ
Ⅲ![]() 证明:
证明:![]() 参考数据:
参考数据:![]() .
.
【答案】(1)0;(2)![]() ;(3)见解析
;(3)见解析
【解析】
(1)求导,由f′(1)=0构造方程求出a;(2)由(1)将方程f(x)+2x=x2+b化简,令g(x)=x2-3x+lnx+b(x>0),求导,研究当x变化时,g′(x),g(x)的变化情况,确定函数的最值,从而建立不等式组,即可求得结论;(3)设φ(x)=lnx-![]() (x2-1),求导,根据函数的单调性得当x≥2时,
(x2-1),求导,根据函数的单调性得当x≥2时,![]() >2
>2![]() ,从而累加可得结论.
,从而累加可得结论.
(1)f′(x)=1-![]() ,∵x=1是f(x)的一个极值点,∴f′(1)=0,即1-
,∵x=1是f(x)的一个极值点,∴f′(1)=0,即1-![]() =0,∴a=0.
=0,∴a=0.
经检验满足题意.
(2)由(1)得f(x)=x-lnx,∴f(x)+2x=x2+b即x-lnx+2x=x2+b,∴x2-3x+lnx+b=0,
设g(x)=x2-3x+lnx+b(x>0),
则g′(x)=2x-3+![]() =
=![]()
=![]() .
.
由g′(x)>0得0<x<![]() 或x>1,由g′(x)<0得
或x>1,由g′(x)<0得![]() <x<1,
<x<1,
∴当x∈![]() ,(1,+∞)时,函数g(x)单调递增,x∈
,(1,+∞)时,函数g(x)单调递增,x∈![]() 时,函数g(x)单调递减,
时,函数g(x)单调递减,
当x=1时,g(x)极小值=g(1)=b-2,g![]() =b-
=b-![]() -ln2,g(2)=b-2+ln2,
-ln2,g(2)=b-2+ln2,
∵方程f(x)+2x=x2+b在![]() 上恰有两个不相等的实数根,
上恰有两个不相等的实数根,
∴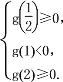 即
即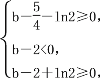 解得
解得![]() +ln2≤b<2.
+ln2≤b<2.
(3)证明:∵k-f(k)=lnk,∴![]()
![]() >
>![]() .
.
![]() +
+![]() +
+![]() +…+
+…+![]() >
>![]() (n∈N,n≥2)
(n∈N,n≥2)
设φ(x)=lnx-![]() (x2-1),则φ′(x)=
(x2-1),则φ′(x)=![]() -
-![]() =
=![]() =-
=-![]()
当x≥2时,φ′(x)<0,∴函数y=φ(x)在[2,+∞)上是减函数,
∴φ(x)≤φ(2)=ln2-![]() <0,∴lnx<
<0,∴lnx<![]() (x2-1).
(x2-1).
∴当x≥2时,![]() >
>![]() =
=![]()
=2![]() ,
,
∴![]() +
+![]() +
+![]() +…+
+…+![]() >2
>2![]()
=2![]() =
=![]() .
.
∴原不等式成立.

 应用题作业本系列答案
应用题作业本系列答案



