题目内容
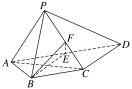
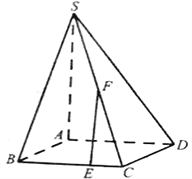
【题目】如图，四边形
是平行四边形，
，
，
，
，
，
.
（1）求证：平面
平面
；
（2）求直线
与平面
所成角的正弦值.
（3）求二面角
的正弦值.
【答案】（1）证明见解析（2）
（3）
【解析】
取AB中点O，推导出
，
，
，从而
平面ABCD，进而
，再求出
，从而
平面AED，由此能证明平面
平面AED；
过A作
于点G，则
即为直线AB与平面BED所成的角，由此能求出直线AB与平面BED所成角的正弦值；
3
二面角
的平面角与二面角
的平面角互补，从而问题转化为求二面角的正弦值，过A作于点G，过A作
于点H，则
即为二面角的平面角，由此能求出二面角的正弦值．
（1）证明：取
中点
，
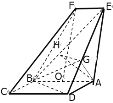
易知四边形
是平行四边形，
则
又
，
，
∴
，
∴
又
，
，
∴
，
∴
又
，
∴
平面
，
∴
在
中，由
得
，
∴
∴
，又
，
∴
面
又
平面
，
∴平面
平面
（2）过
作
于点
，
由（1）知
平面，
则
即为直线与平面所成的角
又
∴
∴直线与平面所成角的正弦值为
（3）∵二面角
的平面角与二面角
的平面角互补，
∴问题转化为求二面角的正弦值
过作于点，过作
于点
，
由（1）知
即切二面角的平面角
∵
∴
又
∴
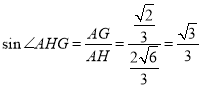
∴二面角的正弦值为.
练习册系列答案
相关题目
【题目】假设关于某设备的使用年限x和所支出的维修费用y（万元）有如下的统计资料：
使用年限x | 2 | 3 | 4 | 5 | 6 |
维修费用y | 2.2 | 3.8 | 5.5 | 6.5 | 7.0 |
若由资料知y对x呈线性相关关系.
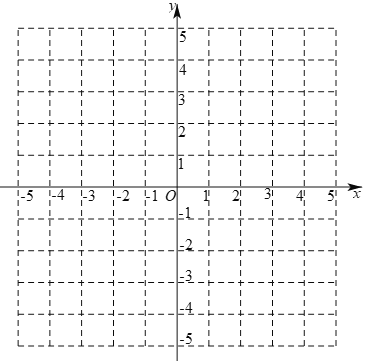
（1）请画出上表数据的散点图；
（2）请根据最小二乘法求出线性回归方程
的回归系数a，b；
（3）估计使用年限为10年时，维修费用是多少？
