题目内容
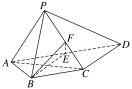
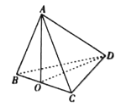
【题目】如图,四棱锥S=ABCD的底面是正方形,SD⊥平面ABCD,SD=AD=a,点E是SD上的点,且DE=![]() a(0<
a(0<![]() ≦1). w.w.w..c.o.m
≦1). w.w.w..c.o.m
(Ⅰ)求证:对任意的![]()
![]() (0、1),都有AC⊥BE:
(0、1),都有AC⊥BE:
(Ⅱ)若二面角C-AE-D的大小为600C,求![]() 的值。
的值。
【答案】(Ⅰ) 略(Ⅱ)![]()
【解析】
运用三垂线定理证明线线垂直,第二问是告诉二面角求参数的值,这是二面角的逆向问题,仍然要作出二面角,求二面角才能解出参数。这题除了用传统的证法与求角的方法外,也可以应用空间向量来解决。
解:(Ⅰ)证发1:连接BD,由底面是正方形可得AC![]() BD。
BD。
![]() SD
SD![]() 平面ABCD,
平面ABCD,![]() BD是BE在平面ABCD上的射影,
BD是BE在平面ABCD上的射影,
由三垂线定理得AC![]() BE.
BE.
(II)解法1:![]() SD
SD![]() 平面ABCD,CD
平面ABCD,CD![]() 平面ABCD,
平面ABCD,![]() SD
SD![]() CD.
CD.
又底面ABCD是正方形,![]() CD
CD![]() AD,又SD
AD,又SD![]() AD=D,
AD=D,![]() CD
CD![]() 平面SAD。
平面SAD。
过点D在平面SAD内做DF![]() AE于F,连接CF,则CF
AE于F,连接CF,则CF![]() AE,
AE,
故![]() CFD是二面角C-AE-D 的平面角,即
CFD是二面角C-AE-D 的平面角,即![]() CFD=60°
CFD=60°
在Rt△ADE中,![]() AD=
AD=![]() , DE=
, DE=![]() , AE=
, AE=![]()
![]() 。
。
于是,DF=![]()
在Rt△CDF中,由![]() cot60°=
cot60°=![]()
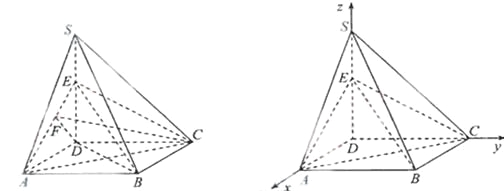
得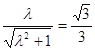 , 即
, 即![]() =3
=3![]() 解得
解得![]() 。
。

练习册系列答案
相关题目
【题目】海水养殖场进行某水产品的新、旧网箱养殖方法的产量对比,收获时各随机抽取了100个网箱,测量各箱水产品的产量(单位:kg), 其频率分布直方图如下:

(1)记A表示事件“旧养殖法的箱产量低于50 kg”,估计A的概率;
(2)填写下面列联表,并根据列联表判断是否有99%的把握认为箱产量与养殖方法有关:
箱产量<50 kg | 箱产量≥50 kg | |
旧养殖法 | ||
新养殖法 |
(3)根据箱产量的频率分布直方图,对这两种养殖方法的优劣进行比较.
附:
P( | 0.050 0.010 0.001 |
k | 3.841 6.635 10.828 |
![]() .
. ![]()