题目内容
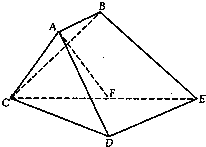 已知多面体ABCDE中,AB⊥平面ACD,DE⊥平面ACD,AC=AD=CD=DE=2,AB=1,F为CE的中点.
已知多面体ABCDE中,AB⊥平面ACD,DE⊥平面ACD,AC=AD=CD=DE=2,AB=1,F为CE的中点.(1)求证:AF⊥CD;
(2)求直线AC与平面CBE所成角的大小.
分析:(1)取CD的中点G,连接AG、GF,则GF∥DE,利用线面垂直的判断性质得到DE⊥CD,GF⊥CD,利用线面垂直的判断得到CD⊥平面AGF,AF?平面AGF得到AF⊥CD.
(2)方法一:建立空间直角坐标系G-xyz,求出平面CBE的法向量,利用向量的数量积公式求出直线AC与平面CBE所成角的大小.
方法二:利用线面垂直的判定定理证得PC⊥平面CDE,得到点A到平面PCE的距离即为点D到平面PCE的距离的一半,通过解三角形求出直线AC与平面CBE所成角的大小.
(2)方法一:建立空间直角坐标系G-xyz,求出平面CBE的法向量,利用向量的数量积公式求出直线AC与平面CBE所成角的大小.
方法二:利用线面垂直的判定定理证得PC⊥平面CDE,得到点A到平面PCE的距离即为点D到平面PCE的距离的一半,通过解三角形求出直线AC与平面CBE所成角的大小.
解答: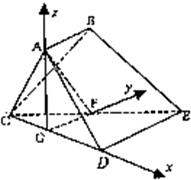 解:法一:(1)取CD的中点G,连接AG、GF,则GF∥DE
解:法一:(1)取CD的中点G,连接AG、GF,则GF∥DE
∵AC=AD,
∴AG⊥GD…(2分)
∵DE⊥平面ACD
∴DE⊥CD
∴GF⊥CD …(4分)
∴CD⊥平面AGF
∵AF?平面AGF
∴AF⊥CD …(6分)
(2)如图建立空间直角坐标系G-xyz,则B(0,1,
),C(-1,0,0),E(1,2,0)
=(1,1,
),
=(2,2,0),
=(1,0,
)
设平面CBE的法向量为
=(x,y,z),
则
设x=1,则
=(1,-1,0)…(9分)
cos<
,
>=
=
 ,
,
∴直线AC与平面CBE所成角的大小为arcsin
…(12分)
法二:(1)同解法一
(2)∵AB⊥平面ACD,DE⊥平面ACD
∴AB∥DE
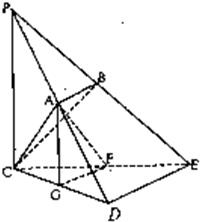
延长DA、EB交于点P,连接PC …(7分)
∵AB=1,DE=2
∴A为PD的中点,又G为CD的中点
∴PC∥AG
∴PC⊥CD,PC⊥DE
∴PC⊥平面CDE …(9分)
∵点A到平面PCE的距离即为点D到平面PCE的距离的一半,
即h=
…(11分)
设直线AC与平面CBE所成角为θ,
则sinθ=
=
,
∴θ=arcsin
…(12分)
 解:法一:(1)取CD的中点G,连接AG、GF,则GF∥DE
解:法一:(1)取CD的中点G,连接AG、GF,则GF∥DE∵AC=AD,
∴AG⊥GD…(2分)
∵DE⊥平面ACD
∴DE⊥CD
∴GF⊥CD …(4分)
∴CD⊥平面AGF
∵AF?平面AGF
∴AF⊥CD …(6分)
(2)如图建立空间直角坐标系G-xyz,则B(0,1,
| 3 |
| CB |
| 3 |
| CE |
| CA |
| 3 |
设平面CBE的法向量为
| n |
则
|
设x=1,则
| n |
cos<
| CA |
| n |
| ||||
|
|
| ||
| 4 |
 ,
,∴直线AC与平面CBE所成角的大小为arcsin
| ||
| 4 |
法二:(1)同解法一
(2)∵AB⊥平面ACD,DE⊥平面ACD
∴AB∥DE
延长DA、EB交于点P,连接PC …(7分)
∵AB=1,DE=2
∴A为PD的中点,又G为CD的中点
∴PC∥AG
∴PC⊥CD,PC⊥DE
∴PC⊥平面CDE …(9分)
∵点A到平面PCE的距离即为点D到平面PCE的距离的一半,
即h=
| ||
| 2 |
设直线AC与平面CBE所成角为θ,
则sinθ=
| h |
| AC |
| ||
| 4 |
∴θ=arcsin
| ||
| 4 |
点评:解决立体几何中的线、面的位置关系或度量关系,常用的方法是通过建立空间直角坐标系,转化为向量的问题来解决.

练习册系列答案
 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案
相关题目
 如图,已知多面体ABCDE中,AE⊥平面ABC,AE
如图,已知多面体ABCDE中,AE⊥平面ABC,AE 如图,已知多面体ABCDE中,AB⊥平面ACD,DE⊥平面ACD,AC=AD=CD=DE=2,AB=1,F为CE的中点.
如图,已知多面体ABCDE中,AB⊥平面ACD,DE⊥平面ACD,AC=AD=CD=DE=2,AB=1,F为CE的中点. 如图,已知多面体ABCDE中,AB⊥面ACD,DE⊥面ACD,三角形ACD是正三角形,且AD=DE=2,AB=1.
如图,已知多面体ABCDE中,AB⊥面ACD,DE⊥面ACD,三角形ACD是正三角形,且AD=DE=2,AB=1. 如图,已知多面体ABCDE中,AB⊥平面ACD,DE∥AB,△ACD是边长为2的正三角形,且DE=2AB=2,F是CD的中点.
如图,已知多面体ABCDE中,AB⊥平面ACD,DE∥AB,△ACD是边长为2的正三角形,且DE=2AB=2,F是CD的中点.