题目内容
(12分)已知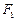 ,
,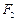 分别是双曲线
分别是双曲线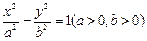 的左右焦点,以坐标原点
的左右焦点,以坐标原点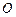 为圆心,以双曲线的半焦距
为圆心,以双曲线的半焦距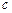 为半径的圆与双曲线在第一象限的交点为
为半径的圆与双曲线在第一象限的交点为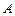 ,与
,与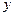 轴正半轴的交点为
轴正半轴的交点为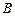 ,点
,点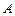 在
在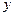 轴上的射影为
轴上的射影为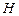 ,且
,且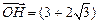
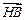 .
.
⑴求双曲线的离心率;
⑵若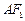 交双曲线于点
交双曲线于点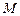 ,且
,且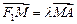 ,求
,求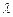 .
.
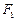 ,
,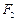 分别是双曲线
分别是双曲线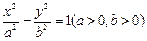 的左右焦点,以坐标原点
的左右焦点,以坐标原点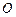 为圆心,以双曲线的半焦距
为圆心,以双曲线的半焦距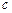 为半径的圆与双曲线在第一象限的交点为
为半径的圆与双曲线在第一象限的交点为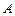 ,与
,与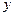 轴正半轴的交点为
轴正半轴的交点为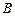 ,点
,点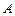 在
在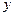 轴上的射影为
轴上的射影为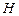 ,且
,且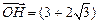
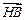 .
.⑴求双曲线的离心率;
⑵若
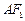 交双曲线于点
交双曲线于点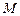 ,且
,且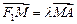 ,求
,求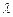 .
.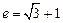 ,
,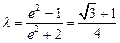
解:⑴由已知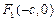 ,
, ,
,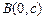 …1分 ∵
…1分 ∵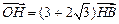 ∴
∴ ,
,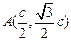 ∵A在双曲线
∵A在双曲线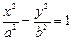 上 ∴
上 ∴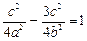 …4分.
…4分.
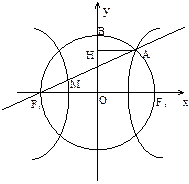

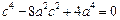
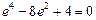
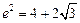 ,
,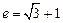 …6分
…6分
⑵∵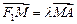 ∴
∴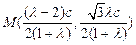 …8分
…8分
由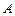 ,
,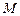 都在双曲线
都在双曲线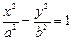 上,
上,
得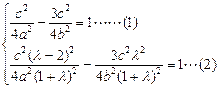
 …10分
…10分
由⑴得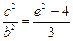 代入⑵
代入⑵ 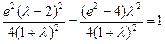
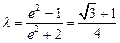 …12分
…12分
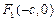 ,
, ,
,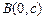 …1分 ∵
…1分 ∵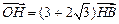 ∴
∴ ,
,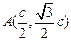 ∵A在双曲线
∵A在双曲线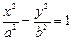 上 ∴
上 ∴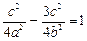 …4分.
…4分.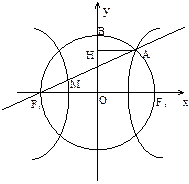

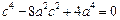
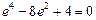
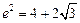 ,
,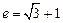 …6分
…6分⑵∵
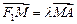 ∴
∴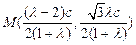 …8分
…8分由
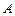 ,
,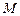 都在双曲线
都在双曲线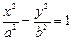 上,
上,得
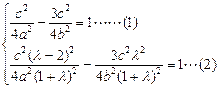
 …10分
…10分由⑴得
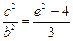 代入⑵
代入⑵ 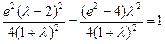
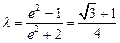 …12分
…12分
练习册系列答案
 品学双优卷系列答案
品学双优卷系列答案 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案 期末复习检测系列答案
期末复习检测系列答案
相关题目
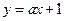 与双曲线C:
与双曲线C: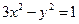 相交于A、B两点.
相交于A、B两点.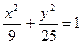 共焦点,它们的离心率之和为
共焦点,它们的离心率之和为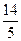 ,求双曲线方程。
,求双曲线方程。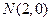 并且与圆
并且与圆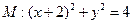 相外切,动圆圆心P的轨迹为W,过点N的直线
相外切,动圆圆心P的轨迹为W,过点N的直线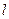 与轨迹W交于A、B两点。
与轨迹W交于A、B两点。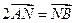 ,求直线
,求直线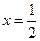 上是否存在一点Q,使得
上是否存在一点Q,使得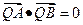 ,并说明理由。
,并说明理由。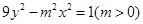 的一个顶点到它的一条渐近线的距离为
的一个顶点到它的一条渐近线的距离为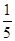 ,则
,则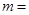 ( )
( )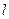 是双曲线
是双曲线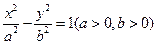 的右准线,以原点O为圆心且过双曲线焦点的圆被直线
的右准线,以原点O为圆心且过双曲线焦点的圆被直线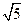
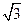
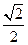
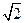
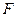 ,虚轴的一个端点为
,虚轴的一个端点为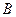 ,如果直线
,如果直线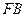 与该双曲线的一条渐近
与该双曲线的一条渐近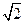
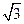
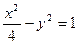 的焦点坐标为( ﹡ ).
的焦点坐标为( ﹡ ). 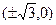
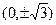

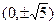
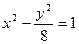 的左焦点F1交双曲线左支于A、B两点,若|AB|=8,则△F2AB的周长为
的左焦点F1交双曲线左支于A、B两点,若|AB|=8,则△F2AB的周长为