题目内容
(本题满分13分)设函数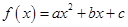 ,且
,且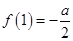 ,
,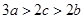 ,求证:(1)
,求证:(1)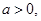 且
且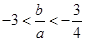 ;
;
(2)函数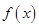 在区间
在区间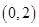 内至少有一个零点;
内至少有一个零点;
(3)设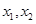 是函数
是函数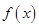 的两个零点,则
的两个零点,则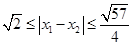 .
.
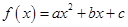 ,且
,且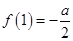 ,
,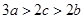 ,求证:(1)
,求证:(1)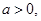 且
且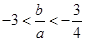 ;
;(2)函数
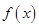 在区间
在区间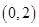 内至少有一个零点;
内至少有一个零点;(3)设
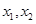 是函数
是函数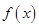 的两个零点,则
的两个零点,则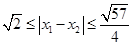 .
.(1)根据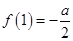 ,求出
,求出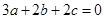 ,再根据
,再根据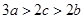 即可得证;(2)先求出
即可得证;(2)先求出 和
和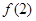 ,根据零点存在定理分
,根据零点存在定理分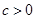 和
和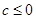 讨论即可得证;
讨论即可得证;
(3)利用韦达定理和第(1)问的结论即可得证.
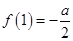 ,求出
,求出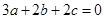 ,再根据
,再根据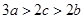 即可得证;(2)先求出
即可得证;(2)先求出 和
和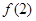 ,根据零点存在定理分
,根据零点存在定理分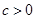 和
和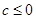 讨论即可得证;
讨论即可得证;(3)利用韦达定理和第(1)问的结论即可得证.
试题分析:(1)
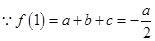 ,
,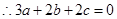 ,
,又
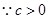 ,
,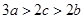 ,
,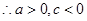 , ……2分
, ……2分又
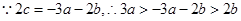
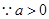
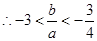 . ……4分
. ……4分(2)
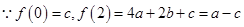
①当
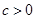 时,
时,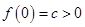 ,
,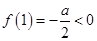
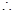 函数
函数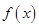 在区间
在区间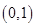 内至少有一个零点
内至少有一个零点②当
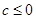 时,
时,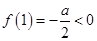 ,
,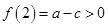 ,
,函数
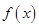 在区间
在区间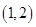 内至少有一个零点
内至少有一个零点综上所述:函数
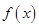 在区间
在区间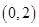 内至少有一个零点。 ……8分
内至少有一个零点。 ……8分(3)
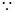
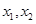 是函数
是函数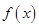 的两个零点,
的两个零点,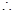
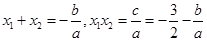
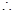
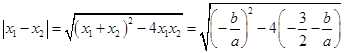
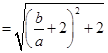
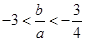 ,
,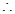
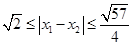 . ……13分
. ……13分点评:证明此类问题时,要充分利用不等式的性质和题设条件,尽量每一步都做到言之有据.

练习册系列答案
 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案
相关题目

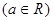
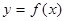 在点
在点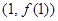 处的切线与
处的切线与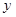 轴和直线
轴和直线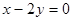 围成的三角形面积等于
围成的三角形面积等于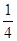 ,求
,求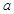 的值;
的值;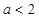 时,讨论
时,讨论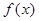 的单调性.
的单调性.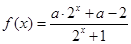
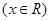 ,若
,若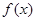 满足
满足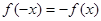 ,
,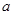 的值; (2)判断函数的单调性,并加以证明。
的值; (2)判断函数的单调性,并加以证明。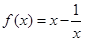 ,对任意
,对任意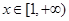 ,
,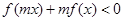 恒成立,则实数
恒成立,则实数 的取值范围是______________.
的取值范围是______________. .
. ,求
,求 的单调区间;
的单调区间; 恒成立,求
恒成立,求 的取值范围.
的取值范围.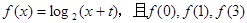 成等差数列,点
成等差数列,点 是函数
是函数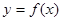 图像上任意一点,点
图像上任意一点,点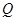 的轨迹是函数
的轨迹是函数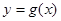 的图像。
的图像。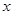 的不等式
的不等式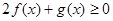 ;
;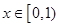 时,总有
时,总有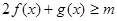 恒成立,求
恒成立,求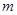 的取值范围。
的取值范围。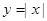 与函数
与函数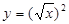 表示同一个函数;
表示同一个函数;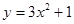 的图像可由
的图像可由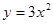 的图像向上平移1个单位得到;
的图像向上平移1个单位得到;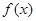 的定义域为
的定义域为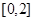 ,则函数
,则函数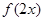 的定义域为
的定义域为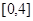 ;
;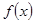 是在区间
是在区间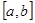 上图象连续的函数,且
上图象连续的函数,且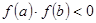 ,则方程
,则方程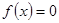 在区间
在区间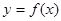 的图像与
的图像与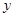 轴的交点个数为 ( )
轴的交点个数为 ( )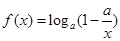 ,其中
,其中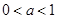 ,
,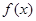 是
是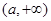 上的减函数;
上的减函数;