题目内容
商场销售的某种饮品每件售价为36元,成本为20元.对该饮品进行促销:顾客每购买一件,当即连续转动三次如图所示转盘,每次停止后指针向一个数字,若三次指向同一个数字,获一等奖;若三次指向的数字是连号(不考虑顺序),获二等奖;其他情况无奖.
(1)求一顾客一次购买两件该饮品,至少有一件获得奖励的概率;
(2)若奖励为返还现金,一等奖奖金数是二等奖的2倍,统计表明:每天的销售y(件)与一等奖的奖金额x(元)的关系式为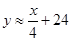 ,问x设定为多少最佳?并说明理由.
,问x设定为多少最佳?并说明理由.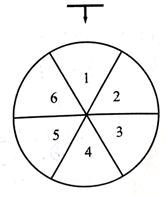
(1)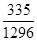 ;(2)x设定为48(元)为最佳.
;(2)x设定为48(元)为最佳.
解析试题分析:本题主要考查随机事件的概率、离散型随机变量的数学期望、配方法求函数最值等基础知识,考查学生的分析问题解决问题的能力、计算能力、转化能力.第一问,先利用活动法则分2种情况分别求出一顾客购买一件饮品获得一等奖和二等奖的概率,2个结果相加得到一顾客购买一件饮品获奖的概率,用间接法在所有概率中去掉2件都没有获奖的概率即可;第二问,先求顾客购买一件饮品所得的奖金额的数学期望,用每件售价-每件的成本-发放的奖金额=每件所得利润,再用这个结果乘以一天卖出的总件数得一天的总利润,再用配方法求函数最值.
(1)记事件:“一顾客购买一件饮品获得i等奖”为Ai,i=1,2,则
P(A1)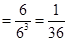 ,P(A2)=
,P(A2)=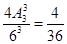 ,
,
则一顾客一次购买一件饮品获得奖励的概率为
P(A1+A2)=P(A1)+P(A2)=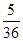 . 4分
. 4分
故一顾客一次购买两件饮品,至少有一件获得奖励的概率
p=1-(1-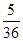 )2=
)2=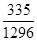 . 6分
. 6分
(2)设一顾客每购买一件饮品所得奖金额为X元,则X的可能取值为x,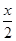 ,0.
,0.
由(1)得P(X=x)= ,P(X=
,P(X=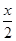 )=
)=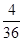 ,E(x)=
,E(x)=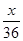 +
+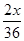 =
=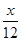 . 9分
. 9分
该商场每天销售这种饮品所得平均利润
Y=y[(36-20)-E(x)]=(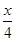 +24)(16-
+24)(16-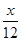 )=-
)=-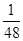 (x-48)2+432.
(x-48)2+432.
当x=48时,Y最大.故x设定为48(元)为最佳. 12分
考点:随机事件的概率、离散型随机变量的数学期望、配方法求函数最值.

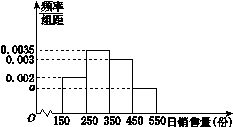
某中学将100名高一新生分成水平相同的甲、乙两个“平行班”,每班50人.陈老师采用A、B两种不同的教学方式分别在甲、乙两个班级进行教改实验.为了了解教学效果,期末考试后,陈老师分别从两个班级中各随机抽取20名学生的成绩进行统计,作出茎叶图如下.记成绩不低于90分者为“成绩优秀”.
| 甲 | | 乙 |
| 6 | 9 | 3 6 7 9 9 |
| 9 5 1 0 | 8 | 0 1 5 6 |
| 9 9 4 4 2 | 7 | 3 4 5 8 8 8 |
| 8 8 5 1 1 0 | 6 | 0 7 7 |
| 4 3 3 2 | 5 | 2 5 |
(1)在乙班样本中的20个个体中,从不低于86分的成绩中随机抽取2个,求抽出的两个均“成绩优秀”的概率;
(2)由以上统计数据填写下面列联表,并判断是否有90%的把握认为:“成绩优秀”与教学方式有关.
| | 甲班(A方式) | 乙班(B方式) | 总计 |
| 成绩优秀 | | | |
| 成绩不优秀 | | | |
| 总计 | | | |
附:
 ,其中n=a+b+c+d.)
,其中n=a+b+c+d.)| P(K2≥k) | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.01 | 0.005 | 0.001 |
| k | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
 的值;
的值; (单位支),当n≥X时,求利润Y的表达式;
(单位支),当n≥X时,求利润Y的表达式;

 表示在这块地上种植1季此作物的利润,求
表示在这块地上种植1季此作物的利润,求 ,求
,求 元,求
元,求
 两条巷道通往作业区(如下图),
两条巷道通往作业区(如下图), 巷道有
巷道有 三个易堵塞点,各点被堵塞的概率都是
三个易堵塞点,各点被堵塞的概率都是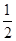 ;
; 巷道有
巷道有 两个易堵塞点,被堵塞的概率分别为
两个易堵塞点,被堵塞的概率分别为 .
.
 ,求
,求 ,并按照"平均堵塞点少的巷道是较好的抢险路线"的标准,请你帮助救援队选择一条抢险路线,并说明理由.
,并按照"平均堵塞点少的巷道是较好的抢险路线"的标准,请你帮助救援队选择一条抢险路线,并说明理由.