题目内容
设抛物线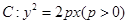 的焦点为
的焦点为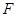 ,经过点
,经过点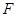 的动直线
的动直线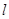 交抛物线
交抛物线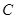 于点
于点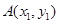 ,
,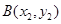 且
且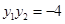 .
.
(1)求抛物线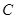 的方程;
的方程;
(2)若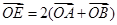 (
(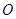 为坐标原点),且点
为坐标原点),且点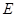 在抛物线
在抛物线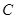 上,求直线
上,求直线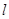 倾斜角;
倾斜角;
(3)若点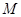 是抛物线
是抛物线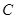 的准线上的一点,直线
的准线上的一点,直线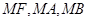 的斜率分别为
的斜率分别为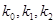 .求证:
.求证:
当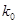 为定值时,
为定值时,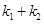 也为定值.
也为定值.
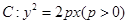 的焦点为
的焦点为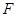 ,经过点
,经过点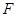 的动直线
的动直线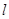 交抛物线
交抛物线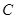 于点
于点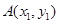 ,
,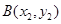 且
且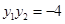 .
.(1)求抛物线
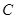 的方程;
的方程;(2)若
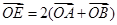 (
(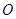 为坐标原点),且点
为坐标原点),且点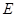 在抛物线
在抛物线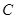 上,求直线
上,求直线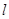 倾斜角;
倾斜角;(3)若点
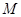 是抛物线
是抛物线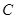 的准线上的一点,直线
的准线上的一点,直线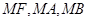 的斜率分别为
的斜率分别为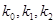 .求证:
.求证:当
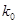 为定值时,
为定值时,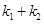 也为定值.
也为定值.(1) (2)倾斜角为
(2)倾斜角为 或
或 (3)
(3)
 (2)倾斜角为
(2)倾斜角为 或
或 (3)
(3)
试题分析:⑴根据题意可知:
 ,设直线
,设直线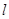 的方程为:
的方程为: ,则:
,则:联立方程:
 ,消去
,消去 可得:
可得: (*),
(*),根据韦达定理可得:
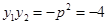 ,∴
,∴ ,∴
,∴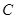 :
:
⑵设
 ,则:
,则: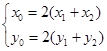 ,由(*)式可得:
,由(*)式可得: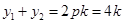
∴
 ,
,又
 ,∴
,∴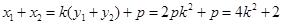
∴

∵
 ,∴
,∴ ,∴
,∴ ,∴
,∴
∴直线
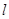 的斜率
的斜率 ,∴倾斜角为
,∴倾斜角为 或
或
⑶可以验证该定值为
 ,证明如下:
,证明如下:设
 ,则:
,则: ,
, ,
,
∵
 ,∴
,∴
∴




∴
 为定值
为定值点评:考查了直线与抛物线的位置关系的运用,体现了运用代数的方法求解解析几何的运用,属于基础题。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
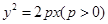 的焦点
的焦点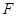 且斜率为
且斜率为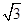 的直线与抛物线交于
的直线与抛物线交于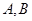 两点,且
两点,且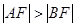 ,则
,则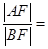 .
.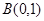 的直线
的直线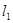 交直线
交直线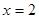 于
于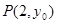 ,过点
,过点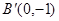 的直线
的直线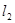 交
交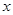 轴于
轴于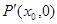 点,
点,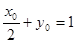 ,
,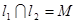 .
.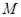 的轨迹
的轨迹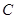 的方程;
的方程;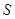 、
、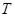 ,已知点
,已知点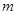 )在线段
)在线段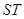 的垂直平分线上且
的垂直平分线上且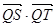 ≤4,求实数
≤4,求实数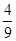 ,求顶点A的轨迹方程.?
,求顶点A的轨迹方程.?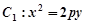 的焦点在抛物线
的焦点在抛物线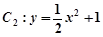 上,点
上,点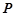 是抛物线
是抛物线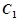 上的动点.
上的动点.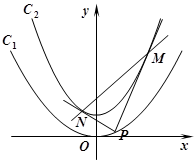
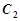 的两条切线,
的两条切线,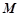 、
、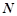 分别为两个切点,设点
分别为两个切点,设点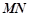 的距离为
的距离为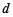 ,求
,求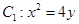 与椭圆
与椭圆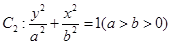 的公共焦点,且椭圆的离心率为
的公共焦点,且椭圆的离心率为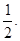
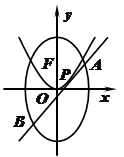
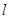 ,切点P在第一象限,如图,设切线
,切点P在第一象限,如图,设切线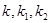 (其中
(其中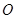 为坐标原点),若
为坐标原点),若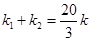 ,求点P的坐标.
,求点P的坐标.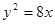 相切倾斜角为
相切倾斜角为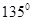 的直线L与x轴和y轴的交点分别是A和B,那么过A、B两点的最小圆截抛物线
的直线L与x轴和y轴的交点分别是A和B,那么过A、B两点的最小圆截抛物线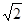 C.2 D.
C.2 D.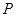 在直线
在直线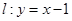 上,若存在过
上,若存在过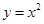 于
于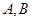 两点,且
两点,且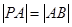 ,则称点
,则称点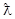 点”,那么下列结论中正确的是( )
点”,那么下列结论中正确的是( )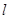 上的所有点都是“
上的所有点都是“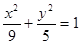 左焦点
左焦点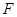 且不垂直于x轴的直线交椭圆于A、B两点,AB的垂直平分线交x轴于点
且不垂直于x轴的直线交椭圆于A、B两点,AB的垂直平分线交x轴于点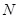 ,则
,则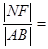 ;
;