题目内容
【题目】已知两定点![]() ,
, ![]() ,曲线
,曲线![]() 上的动点
上的动点![]() 满足
满足![]() ,直线
,直线![]() 与曲线
与曲线![]() 的另一个交点为
的另一个交点为![]() .
.
(Ⅰ)求曲线![]() 的标准方程;
的标准方程;
(Ⅱ)设点![]() ,若
,若![]() ,求直线
,求直线![]() 的方程.
的方程.
【答案】(Ⅰ)![]() (Ⅱ)
(Ⅱ)![]()
【解析】试题分析:(Ⅰ)由题意知|MF1|+|MF2|=2|F1F2|=8>4,所以曲线C是以F1,F2为焦点,长轴长为8的椭圆.由此可知曲线C的方程;(Ⅱ)设M(xM,yM),P(xP,yP),直线MN方程为y=k(x+4),其中k≠0.由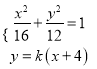 得(3+4k2)y2-24ky=0,由此利用韦达定理、椭圆性质,结合已知条件
得(3+4k2)y2-24ky=0,由此利用韦达定理、椭圆性质,结合已知条件![]() ,所以
,所以![]() ,则
,则![]() ,转化为坐标关系求出点
,转化为坐标关系求出点![]() 坐标代入椭圆即可.
坐标代入椭圆即可.
试题解析:
(Ⅰ)∵![]() ,
, ![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴曲线![]() 是以
是以![]() ,
, ![]() 为焦点,长轴长为
为焦点,长轴长为![]() 的椭圆.
的椭圆.
曲线![]() 的方程为
的方程为![]() .
.
(Ⅱ)由题意知直线![]() 不垂直于
不垂直于![]() 轴,也不与
轴,也不与![]() 轴重合或平行.
轴重合或平行.
设![]() ,
, ![]() ,直线
,直线![]() 方程为
方程为![]() ,其中
,其中![]() .
.
由 ,得
,得![]() .
.
解得![]() 或
或![]() .
.
依题意![]() ,
, ![]() .
.
因为![]() ,
,
所以![]() ,则
,则![]() .
.
于是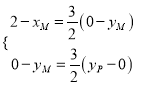 ,所以
,所以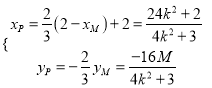 ,
,
因为点![]() 在椭圆上,所以
在椭圆上,所以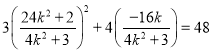 .
.
整理得![]() ,
,
解得![]() 或
或![]() (舍去),
(舍去),
从而![]() .
.
所以直线![]() 的方程为
的方程为![]() .
.

练习册系列答案
 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案
相关题目
