题目内容
【题目】已知函数f(x)=2x3+bx2+cx,其导函数y=f′(x)的图象(如图所示)经过点(1,0),(2,0). (Ⅰ)求f(x)的解析式;
(Ⅱ)若方程f(x)﹣m=0恰有2个根,求m的值.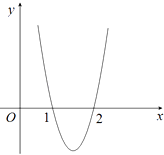
【答案】解:(Ⅰ)依题意,可得f'(x)=6x2+2bx+c=0的解为x=1,x=2, 故 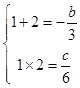 解得
解得 ![]()
所以f(x)=2x3﹣9x2+12x.
(Ⅱ)f'(x)=6x2﹣18x+12=6(x﹣1)(x﹣2),
当f'(x)>0时,x<1或x>2;
当f'(x)<0时,1<x<2.
所以函数f(x)的单调增区间为(﹣∞,1)和(2,+∞),单调减区间为(1,2),
当x=1时,f(x)极大=5,当x=2时,f(x)极小=4.
故方程f(x)﹣m=0恰有2个根,得m=4或m=5
【解析】(Ⅰ)根据图象可得得f'(x)=6x2+2bx+c=0的解为x=1,x=2,根据根与系数的关系,联立方程组求解即可;(Ⅱ)根据导数求出函数的单调区间,求出相应函数值,即可求实数m的值.
【考点精析】利用基本求导法则和利用导数研究函数的单调性对题目进行判断即可得到答案,需要熟知若两个函数可导,则它们和、差、积、商必可导;若两个函数均不可导,则它们的和、差、积、商不一定不可导;一般的,函数的单调性与其导数的正负有如下关系: 在某个区间![]() 内,(1)如果
内,(1)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递增;(2)如果
在这个区间单调递增;(2)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递减.
在这个区间单调递减.

练习册系列答案
相关题目