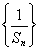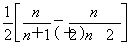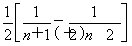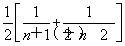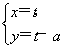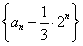Question

在极坐标系中，曲线C：ρ＝msin θ(m>0)，若极轴上的点P(2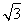，0)与曲线C上任意两点的连线所成的最大夹角是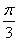，则m＝________.

 

Answer 1

m＝4

【解析】曲线C：ρ＝msin θ(m>0)化为直角坐标方程是x2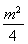＋＝，极轴上的点P(2，0)在直角坐标系中对应的点的坐标仍为P(2，0)．如图，在直角坐标系中，点P与曲线C上任意两点的连线所成的最大夹角是过点P的两条切线所成的角．易知x轴是圆的一条切线，且∠OPC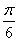＝，所以OP＝·OC，即·＝2，解得m＝4