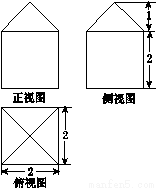
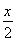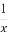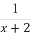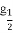题目内容
已知数列{an}的相邻两项an，an＋1是关于x的方程x2－2nx＋bn＝0的两根，且a1＝1.
(1)求证：数列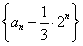
是等比数列；
(2)求数列{an}的前n项和Sn；
(3)设函数f(n)＝bn－t·Sn(n∈N*)，若f(n)＞0对任意的n∈N*都成立，求t的取值范围．
（1）见解析（2）
（3）t＜1
【解析】(1)∵an＋an＋1＝2n，∴an＋1－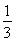
·2n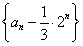＋1＝－
，
＝－1，∴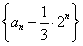
是等比数列，
又a1－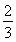
＝
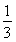，q＝－1，∴an＝
[2n－(－1)n]．
(2)由(1)得Sn＝a1＋a2＋…＋an
＝
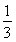(2＋22＋…＋2n)－
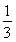[(－1)＋(－1)2＋…＋(－1)n]＝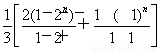
＝
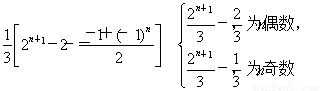
(3)∵bn＝an·an＋1，
∴bn＝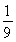
[2n－(－1)n][2n＋1－(－1)n＋1]＝
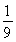[22n＋1－(－2)n－1]，∴bn－t·Sn＞0，
∴
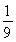[22n＋1－(－2)n－1]－t·
＞0，∴当n为奇数时，
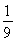(22n＋1＋2n－1)－
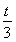(2n＋1－1)＞0，∴t＜
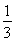(2n＋1)对任意的n为奇数都成立，∴t＜1.
∴当n为偶数时，
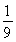(22n＋1－2n－1)－
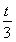(2n＋1－2)＞0，
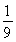∴ (22n＋1－2n－1)－
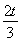(2n－1)＞0，
∴t＜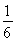
(2n＋1＋1)对任意的n为偶数都成立，∴t＜
.
综上所述，t的取值范围为t＜1
练习册系列答案
相关题目
