题目内容
13.已知a,b,c,d∈(0,+∞),求证ac+bd≤$\sqrt{{(a}^{2}+{b}^{2})({c}^{2}+{d}^{2})}$.分析 法一:利用分析法逐步推出0≤(bc-ad)2,得到结果即可.
法二:利用综合法,通过利用重要不等式,证明即可.
解答 (本小题满分10分)
证明:法一:(分析法)
a,b,c,d∈(0,+∞),欲证ac+bd≤$\sqrt{{(a}^{2}+{b}^{2})({c}^{2}+{d}^{2})}$,只需证(ac+bd)2≤(a2+b2)(c2+d2),
即证a2c2+2abcd+b2d2≤a2c2+b2d2+a2d2+b2c2,即证2abcd≤a2d2+b2c2,
即证0≤(bc-ad)2,而a,b,c,d∈(0,+∞),0≤(bc-ad)2显然成立,
故原不等式成立.
法二:(综合法)(a2+b2)(c2+d2)=a2c2+b2d2+a2d2+b2c2≥a2c2+b2d2+2abcd
=(ac+bd)2,所以$\sqrt{{(a}^{2}+{b}^{2})({c}^{2}+{d}^{2})}$≥ac+bd.
点评 本题考查不等式的证明,考查分析法与综合法的应用,考查逻辑推理能力.

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目
1.定积分$\int_{-2π}^{2π}{({2x-sinx})}$的值为( )
| A. | -1 | B. | 0 | C. | 1 | D. | 2 |
3.定义在R上的函数f(x)满足f(x+1)=2f(x),且当x∈(0,1)时,f(x)=4x,则f(5.5)=( )
| A. | 32 | B. | $\frac{129}{4}$ | C. | 64 | D. | 16 |
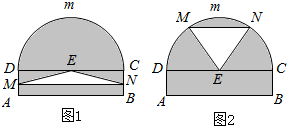 某仓库为了保持库内的湿度和温度,四周墙上均装有如图所示的自动通风设施.该设施的下部ABCD是矩形,其中AB=2米,BC=0.5米.上部CmD是个半圆,固定
某仓库为了保持库内的湿度和温度,四周墙上均装有如图所示的自动通风设施.该设施的下部ABCD是矩形,其中AB=2米,BC=0.5米.上部CmD是个半圆,固定