题目内容
【题目】(本小题共![]() 分)
分)
若![]() 或
或![]() ,则称
,则称![]() 为
为![]() 和
和![]() 的一个
的一个![]() 位排列,对于
位排列,对于![]() ,将排列
,将排列![]() 记为
记为![]() ,将排列
,将排列![]() 记为
记为![]() ,依此类推,直至
,依此类推,直至![]() ,对于排列
,对于排列![]() 和
和![]() ,它们对应位置数字相同的个数减去对应位置数字不同的数,叫做
,它们对应位置数字相同的个数减去对应位置数字不同的数,叫做![]() 和
和![]() 的相关值,记作
的相关值,记作![]() ,例如
,例如![]() ,则
,则![]() ,
,![]() ,若
,若![]() ,则称
,则称![]() 为最佳排列.
为最佳排列.
(Ⅰ)写出所有的最佳排列![]() .
.
(Ⅱ)证明:不存在最佳排列![]() .
.
(Ⅲ)若某个![]() (
(![]() 是正整数)为最佳排列,求排列
是正整数)为最佳排列,求排列![]() 中
中![]() 的个数.
的个数.
【答案】详见解析
【解析】
试题分析:(Ⅰ)根据最佳排列的定义可得,最佳排列![]() 为
为![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() ;(Ⅱ)由
;(Ⅱ)由![]() ,可得
,可得![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 之中有
之中有![]() 个
个![]() ,
,![]() 个
个![]() ,而
,而![]() 经过奇数次数码改变不能回到自身,所以不存在
经过奇数次数码改变不能回到自身,所以不存在![]() ,使得
,使得![]() ;(Ⅲ)
;(Ⅲ)![]() 与每个人
与每个人![]() 有
有![]() 个对应位置数码相同,有
个对应位置数码相同,有![]() 个对应位置数码不同,设
个对应位置数码不同,设![]() ,
, ![]() ,
,![]() 中有
中有![]() 个
个![]() ,
,![]() 个
个![]() ,则
,则![]() ,可得
,可得![]() ,解得
,解得![]() 或
或![]() ,从而得出结论.
,从而得出结论.
试题解析:(Ⅰ)最佳排列![]() 为
为![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() .
.
(Ⅱ)设![]() ,则
,则![]() ,
,
因为![]() ,
,
所以![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 之中有
之中有![]() 个
个![]() ,
,![]() 个
个![]() ,
,
按![]() 的顺序研究数码变化,
的顺序研究数码变化,
有上述分析可知由![]() 次数码不发生改变,有
次数码不发生改变,有![]() 次数码发生了改变,
次数码发生了改变,
但是![]() 经过奇数次数码改变不能回到自身,
经过奇数次数码改变不能回到自身,
所以不存在![]() ,
,
使得![]() ,
,
从而不存在最佳排列![]() .
.
(Ⅲ)由![]() 或
或![]() ,
,![]() ,
,![]() ,
,![]() ,
,
得![]() ,
,![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
以上各式求和得,![]() ,
,
另一方面,![]() 还可以这样求和:设
还可以这样求和:设![]() ,
, ![]() ,
,![]() 中有
中有![]() 个
个![]() ,
,![]() 个
个![]() ,
,
则![]() ,
,
所以![]() ,
,
得![]() 或
或![]() ,
,
所以排列![]() 中
中![]() 的个数是
的个数是![]() 或
或![]() 个.
个.

【题目】某厂生产不同规格的一种产品,根据检测标准,其合格产品的质量![]() 与尺寸
与尺寸![]() 之间近似满足关系式
之间近似满足关系式![]() 为大于0的常数).按照某项指标测定,当产品质量与尺寸的比在区间
为大于0的常数).按照某项指标测定,当产品质量与尺寸的比在区间![]() 内时为优等品.现随机抽取6件合格产品,测得数据如下:
内时为优等品.现随机抽取6件合格产品,测得数据如下:
尺寸 | 38 | 48 | 58 | 68 | 78 | 88 |
质量 | 16.8 | 18.8 | 20.7 | 22.4 | 24 | 25.5 |
质量与尺寸的比 | 0.442 | 0.392 | 0.367 | 0.329 | 0.308 | 0.290 |
(I)现从抽取的6件合格产品中再任选3件,记![]() 为取到优等品的件数,试求随机变量
为取到优等品的件数,试求随机变量![]() 的分布列和期望;
的分布列和期望;
(II)根据测得数据作了初步处理,得相关统计量的值如下表:
|
|
|
|
75.3 | 24.6 | 18.3 | 101.4 |
(i)根据所给统计量,求![]() 关于
关于![]() 的回归方程;
的回归方程;
(ii)已知优等品的收益![]() (单位:千元)与
(单位:千元)与![]() 的关系为
的关系为![]() ,则当优等品的尺寸
,则当优等品的尺寸![]() 为何值时,收益
为何值时,收益![]() 的预报值最大? (精确到0.1)
的预报值最大? (精确到0.1)
附:对于样本![]() , 其回归直线
, 其回归直线![]() 的斜率和截距的最小二乘估计公式分别为:
的斜率和截距的最小二乘估计公式分别为:
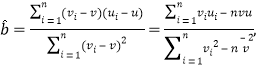
![]()
![]()
【题目】某出租车公司为了解本公司出租车司机对新法规的知晓情况,随机对100名出租车司机进行调查.调查问卷共10道题,答题情况如下表:
答对题目数 |
| 8 | 9 |
|
女 | 2 | 13 | 12 | 8 |
男 | 3 | 37 | 16 | 9 |
(1)如果出租车司机答对题目数大于等于9,就认为该司机对新法规的知晓情况比较好,试估计该公司的出租车司机对新法规知晓情况比较好的概率;
(2)从答对题目数少于8的出租车司机中任选出两人做进一步的调查,求选出的两人中至少有一名女出租车司机的概率.
