题目内容
11.已知A={x|x2+2x-8=0},B={x|x2-5x+8=2},C={x|x2-ax+a2-19=0};若A∩C=∅,B∩C≠∅,求a的值.分析 求解一元二次方程化简集合A,B,结合已知可知3∈C,把x=3代入x2-ax+a2-19=0求得a值,然后再分别求解集合C,验证A∩C后得答案.
解答 解:A={x|x2+2x-8=0}={2,-4},B={x|x2-5x+8=2}={2,3},
由A∩C=∅,知2∉C,-4∉C,
又由B∩C≠∅,知3∈C,
∴32-3a+a2-19=0,解得a=-2或a=5,
当a=-2时,C={3,-5},满足A∩C=∅,
当a=5时,C={3,2},A∩C={2}≠∅舍去,
∴a=-2.
点评 本题考查交集及其运算,考查元素与集合间的关系,是基础题.

练习册系列答案
相关题目
9.已知角α的顶点与原点重合,始边与x轴的正半轴重合,终边经过点P(-3,m),且sinα=-$\frac{4}{5}$,则tanα等于( )
| A. | -$\frac{4}{3}$ | B. | $\frac{4}{3}$ | C. | $\frac{3}{4}$ | D. | -$\frac{3}{4}$ |
2.用数学归纳法证明“1+2+…+n+(n-1)…+2+1=n2(n∈N+)”,从n=k到n=k+1时,左边添加的代数式为( )
| A. | k+1 | B. | k+2 | C. | k+1+k | D. | 2(k+1) |
3.下列四组函数中,表示同一函数的是( )
| A. | y=x-1与y=$\sqrt{(x-1)^{2}}$ | B. | y=$\sqrt{x-1}$与y=$\frac{x-1}{\sqrt{x-1}}$ | ||
| C. | y=lgx-2与y=lg$\frac{x}{100}$ | D. | y=4lgx与y=lgx2 |
20.函数f(x)=$\frac{1}{x}-x+{x^3}$的图象关于( )
| A. | y轴对称 | B. | 直线y=x对称 | C. | 坐标原点对称 | D. | 直线y=-x对称 |
1.已知y=cos(ωx+φ)(ω>0,φ∈[0,2π))的部分图象如图所示,则φ=( )
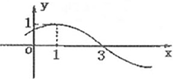

| A. | $\frac{3π}{2}$ | B. | $\frac{7π}{4}$ | C. | $\frac{π}{4}$ | D. | 0 |