题目内容
16.若函数f(x)=$\left\{\begin{array}{l}{2{x}^{3}+3{x}^{2}+1,x≤0}\\{-{x}^{2}+2ax-{a}^{2}+2a,x>0}\end{array}\right.$在区间[-2,2]上的最大值为2,则实数a的取值范围是(-∞,1]∪[3+$\sqrt{3}$,+∞).分析 运用导数,求得当x∈[-2,0]上的最大值为2; 欲使得函数f(x)在[-2,2]上的最大值为2,讨论f(x)在(0,2]上的最大值必须小于等于2,解不等式从而可得a的范围.
解答 解:由题意,当x≤0时,f(x)=2x3+3x2+1,
可得f′(x)=6x2+6x,
由函数在[-1,0]上导数为负,在[-∞,-1]上导数为正,
故函数在[-2,0]上的最大值为f(-1)=2;
要使函数f(x)=$\left\{\begin{array}{l}{2{x}^{3}+3{x}^{2}+1,x≤0}\\{-{x}^{2}+2ax-{a}^{2}+2a,x>0}\end{array}\right.$在[-2,2]上的最大值为2,
则当x>0时,f(x)=-(x-a)2+2a,对称轴为x=a,
当a≤0时,区间(0,2]为减区间,f(0)=2a≤0;
当0<a<2时,f(a)取得最大,且为2a≤2,解得0<a≤1;
当a≥2时,区间(0,2]为增区间,f(2)=-4+6a-a2≤2,
解得a≥3+$\sqrt{3}$.
综上可得a的范围是a≥3+$\sqrt{3}$或a≤1.
故答案为:(-∞,1]∪[3+$\sqrt{3}$,+∞).
点评 本小题主要考查函数单调性的应用、函数最值的应用、不等式的解法等基础知识,考查运算求解能力,考查化归与转化思想.属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
6.某车间为了规定工时定额,需要确定加工零件所花费的时间,为此作了四次试验,得到的数据如下:
y关于x的线性回归方程$\widehat{y}$=$\widehat{a}x+\widehat{b}$为$\hat{y}$=0.7x+1.05.
| 零件的个数x(个) | 2 | 3 | 4 | 5 |
| 加工的时间y(小时) | 2.5 | 3 | 4 | 4.5 |
4.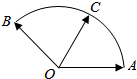 给定两个长度为1的平面向量$\overrightarrow{OA}$和$\overrightarrow{OB}$,它们的夹角为120°如图所示,点C在以O为圆心的圆弧$\overrightarrow{AB}$上变动.若$\overrightarrow{OC}$=x$\overrightarrow{OA}$+y$\overrightarrow{OB}$,其中x,y∈R,则x+y的最大值是( )
给定两个长度为1的平面向量$\overrightarrow{OA}$和$\overrightarrow{OB}$,它们的夹角为120°如图所示,点C在以O为圆心的圆弧$\overrightarrow{AB}$上变动.若$\overrightarrow{OC}$=x$\overrightarrow{OA}$+y$\overrightarrow{OB}$,其中x,y∈R,则x+y的最大值是( )
 给定两个长度为1的平面向量$\overrightarrow{OA}$和$\overrightarrow{OB}$,它们的夹角为120°如图所示,点C在以O为圆心的圆弧$\overrightarrow{AB}$上变动.若$\overrightarrow{OC}$=x$\overrightarrow{OA}$+y$\overrightarrow{OB}$,其中x,y∈R,则x+y的最大值是( )
给定两个长度为1的平面向量$\overrightarrow{OA}$和$\overrightarrow{OB}$,它们的夹角为120°如图所示,点C在以O为圆心的圆弧$\overrightarrow{AB}$上变动.若$\overrightarrow{OC}$=x$\overrightarrow{OA}$+y$\overrightarrow{OB}$,其中x,y∈R,则x+y的最大值是( )| A. | $\sqrt{2}$ | B. | 2 | C. | $\sqrt{3}$ | D. | 3 |
11.设函数f(x)=ln(1+x),g(x)=$\frac{ax}{1+x}$(x≥0),若f(x)≥g(x)恒成立,则a的取值范围是( )
| A. | a≤2 | B. | a≥2 | C. | a≤1 | D. | a≥1 |
8.执行如图所示的程序框图,如果输入a=1,b=3,则输出的a的值为( )
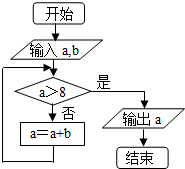

| A. | 7 | B. | 9 | C. | 10 | D. | 13 |
6.甲、乙两歼击机的飞行员向同一架敌机射击,设击中的概率分别为0.4,0.5,则恰有一人击中敌机的概率为( )
| A. | 0.9 | B. | 0.2 | C. | 0.7 | D. | 0.5 |