题目内容
函数f(x)=x3-3ax+b(a>0)的极大值为6,极小值为2,则f(x)的单调递减区间是______.
(-1,1)
【解析】令f′(x)=3x2-3a=0,得x= 或-
或-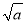 .
.
f(x),f′(x)随x的变化情况如下表:
x | (-∞,- | - | (- |
| ( |
f′(x) | + | 0 | - | 0 | + |
f(x) | ? | 极大值 | ? | 极小值 | ? |
从而 得
得 所以f(x)的单调递减区间是(-1,1).
所以f(x)的单调递减区间是(-1,1).

练习册系列答案
 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案
相关题目
题目内容
函数f(x)=x3-3ax+b(a>0)的极大值为6,极小值为2,则f(x)的单调递减区间是______.
(-1,1)
【解析】令f′(x)=3x2-3a=0,得x= 或-
或-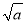 .
.
f(x),f′(x)随x的变化情况如下表:
x | (-∞,- | - | (- |
| ( |
f′(x) | + | 0 | - | 0 | + |
f(x) | ? | 极大值 | ? | 极小值 | ? |
从而 得
得 所以f(x)的单调递减区间是(-1,1).
所以f(x)的单调递减区间是(-1,1).

 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案