题目内容
(本小题满分13分)如图,椭圆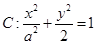 的焦点在
的焦点在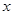 轴上,左、右顶点分别为
轴上,左、右顶点分别为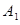 、
、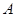 ,上顶点为
,上顶点为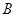 ,抛物线
,抛物线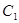 、
、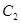 分别以
分别以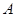 、
、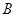 为焦点,其顶点均为坐标原点
为焦点,其顶点均为坐标原点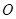 ,
,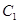 与
与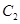 相交于直线
相交于直线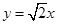 上一点
上一点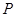 .
.
(Ⅰ)求椭圆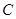 及抛物线
及抛物线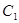 、
、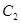 的方程;
的方程;
(Ⅱ)若动直线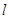 与直线
与直线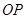 垂直,且与椭圆
垂直,且与椭圆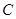 交于不同的两点
交于不同的两点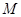 、
、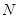 ,已知点
,已知点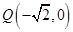 ,求
,求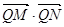 的最小值.
的最小值. 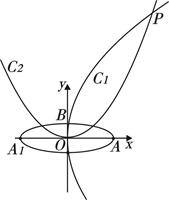
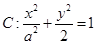 的焦点在
的焦点在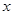 轴上,左、右顶点分别为
轴上,左、右顶点分别为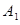 、
、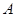 ,上顶点为
,上顶点为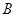 ,抛物线
,抛物线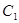 、
、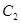 分别以
分别以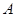 、
、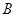 为焦点,其顶点均为坐标原点
为焦点,其顶点均为坐标原点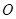 ,
,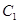 与
与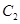 相交于直线
相交于直线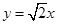 上一点
上一点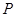 .
.(Ⅰ)求椭圆
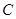 及抛物线
及抛物线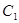 、
、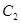 的方程;
的方程;(Ⅱ)若动直线
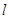 与直线
与直线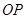 垂直,且与椭圆
垂直,且与椭圆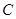 交于不同的两点
交于不同的两点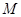 、
、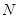 ,已知点
,已知点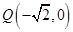 ,求
,求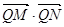 的最小值.
的最小值. 
(Ⅰ)椭圆C: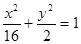 ,抛物线C1:
,抛物线C1: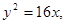 抛物线C2:
抛物线C2: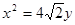 ;
;
(Ⅱ)其最小值等于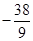 .
.
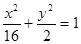 ,抛物线C1:
,抛物线C1: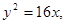 抛物线C2:
抛物线C2: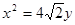 ;
;(Ⅱ)其最小值等于
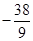 .
.(1)根据点P是三条曲线的交点,利用方程组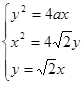 可解出P点坐标及a的值。
可解出P点坐标及a的值。
(2)设直线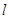 方程为
方程为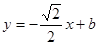 ,然后与椭圆方程联立,消y得一元二次方程利用违达定得代入
,然后与椭圆方程联立,消y得一元二次方程利用违达定得代入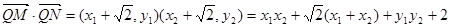 可建立关于b的方程,解出b再验证判断式即可。
可建立关于b的方程,解出b再验证判断式即可。
解:(Ⅰ)由题意,A(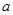 ,0),B(0,
,0),B(0,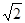 ),故抛物线C1的方程可设为
),故抛物线C1的方程可设为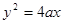 ,C2的方程为
,C2的方程为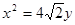 …………………………1分
…………………………1分
由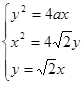 得
得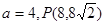 …………………………3分
…………………………3分
所以椭圆C: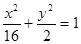 ,抛物线C1:
,抛物线C1: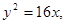 抛物线C2:
抛物线C2: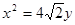 …………5分
…………5分
(Ⅱ)由(Ⅰ)知,直线OP的斜率为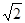 ,所以直线
,所以直线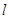 的斜率为
的斜率为
设直线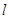 方程为
方程为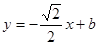
由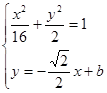 ,整理得
,整理得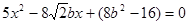 …………………… 6分
…………………… 6分
因为动直线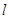 与椭圆C交于不同两点,所以
与椭圆C交于不同两点,所以
解得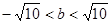 …………………………7分
…………………………7分
设M(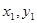 )、N(
)、N(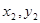 ),则
),则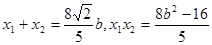
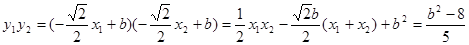 ……8分
……8分
因为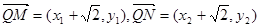
所以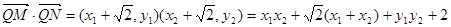
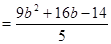 ………………………… 11分
………………………… 11分
因为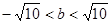 ,所以当
,所以当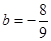 时,
时,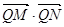 取得最小值
取得最小值
其最小值等于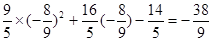 …………………………13分
…………………………13分
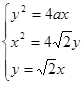 可解出P点坐标及a的值。
可解出P点坐标及a的值。(2)设直线
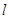 方程为
方程为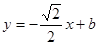 ,然后与椭圆方程联立,消y得一元二次方程利用违达定得代入
,然后与椭圆方程联立,消y得一元二次方程利用违达定得代入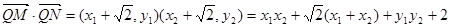 可建立关于b的方程,解出b再验证判断式即可。
可建立关于b的方程,解出b再验证判断式即可。解:(Ⅰ)由题意,A(
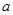 ,0),B(0,
,0),B(0,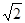 ),故抛物线C1的方程可设为
),故抛物线C1的方程可设为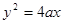 ,C2的方程为
,C2的方程为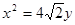 …………………………1分
…………………………1分由
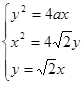 得
得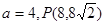 …………………………3分
…………………………3分所以椭圆C:
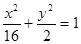 ,抛物线C1:
,抛物线C1: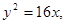 抛物线C2:
抛物线C2: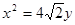 …………5分
…………5分(Ⅱ)由(Ⅰ)知,直线OP的斜率为
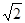 ,所以直线
,所以直线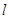 的斜率为
的斜率为
设直线
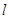 方程为
方程为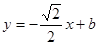
由
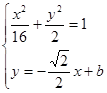 ,整理得
,整理得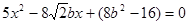 …………………… 6分
…………………… 6分因为动直线
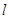 与椭圆C交于不同两点,所以
与椭圆C交于不同两点,所以
解得
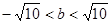 …………………………7分
…………………………7分设M(
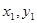 )、N(
)、N(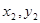 ),则
),则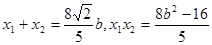
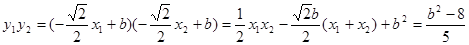 ……8分
……8分因为
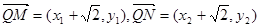
所以
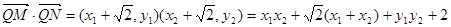
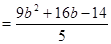 ………………………… 11分
………………………… 11分因为
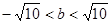 ,所以当
,所以当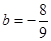 时,
时,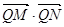 取得最小值
取得最小值其最小值等于
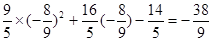 …………………………13分
…………………………13分
练习册系列答案
相关题目
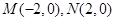 ,动点
,动点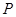 满足条件
满足条件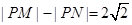 .记动点
.记动点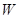 .
.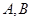 是
是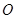 是坐标原点,求
是坐标原点,求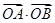 的最小值.
的最小值.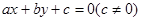 与抛物线
与抛物线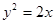 交于P、Q两点,F为抛物线的焦点,直线PF,QF分别交抛物线点M、N,则直线MN的方程为 。
交于P、Q两点,F为抛物线的焦点,直线PF,QF分别交抛物线点M、N,则直线MN的方程为 。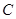 :
: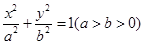 的离心率为
的离心率为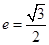 ,且过点
,且过点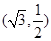 .
.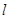 与椭圆
与椭圆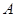 、
、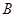 两点,若以
两点,若以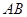 为直径的圆
为直径的圆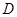 经过坐标原点.证明:圆
经过坐标原点.证明:圆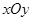 中,已知点
中,已知点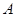
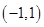 ,P是动点,且三角形
,P是动点,且三角形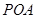 的三边所在直线的斜率满足
的三边所在直线的斜率满足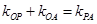 .
.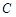 的方程;
的方程;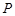 的一个点,且
的一个点,且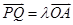 ,直线
,直线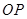 与
与 交于点M,试探
交于点M,试探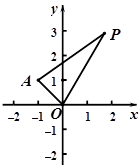
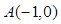 ,
,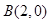 ,动点满足条件
,动点满足条件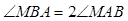 ,动点
,动点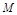 的轨迹方程是 .
的轨迹方程是 .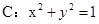 ,过点
,过点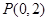 作圆C的切线,交x轴正半轴于点Q.若
作圆C的切线,交x轴正半轴于点Q.若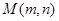 为线段PQ(不包括端点)上的动点,则
为线段PQ(不包括端点)上的动点,则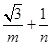 的最小值为_____ .
的最小值为_____ .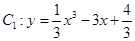 ,曲线
,曲线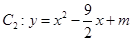 ,若当
,若当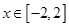 时,曲线
时,曲线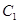 在曲线
在曲线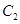 的下方,则实数
的下方,则实数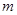 的取值范围是 .
的取值范围是 .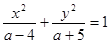 的焦点为定点,则焦点坐标是 .
的焦点为定点,则焦点坐标是 .