Question

已知椭圆

x2

a2

+

y2

b2

=1（a＞b＞0）的离心率为

2

2

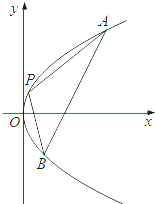
，F₁，F₂分别是椭圆的左、右焦点，过点F₂与x轴不垂直的直线l交椭圆于A、B两点，则△ABF₁的周长为4

2

．
（1）求椭圆的方程；
（2）若C（

1

3

，0），使得|AC|=|BC|，求直线l的方程．

Answer 1

（1）∵椭圆

x2

a2

+

y2

b2

=1（a＞b＞0）的离心率为

2

2

，
F₁，F₂分别是椭圆的左、右焦点，
过点F₂与x轴不垂直的直线l交椭圆于A、B两点，△ABF₁的周长为4

2

，
∴

c a = 2 2 4a=4 2

，∴a=

2

，c=1，∴b=1，
∴椭圆方程为

x2

2

+y2=1．
（2）∵过点F₂（1，0）与x轴不垂直的直线l交椭圆于A、B两点，
∴设直线AB的方程为x=ny+1，
联立

x=ny+1 x2 2 +y2=1

，得（2+n²）y²+2ny-1=0，
△=4n²+4（2+n²）＞0，
设A（x₁，y₁），B（x₂，y₂），则y₁+y₂=

-2n

2+n2

，y₁y₂=

-1

2+n2

，
∴x₁+x₂=n（y₁+y₂）+2=

-2n2

2+n2

+2
∵C（

1

3

，0）使得|AC|=|BC|，
∴

(x1- 1 3 )2+y12

=

(x2- 1 3 )2+y22

，
∴x12-

2

3

x1+y12=x22-

2

3

x2+y22，
整理，得（x₁+x₂-

2

3

）（x₁-x₂）+（y₁+y₂）（y₁-y₂）=0，
∴k=

y1-y2

x1-x2

=

x1+x2- 2 3

-(y1+y2)

=

-2n2 2+n2 +2- 2 3

2n 2+n2

=

4

3n

-

n

3

，
∵k=

1

n

，∴

1

n

=

4

3n

-

n

3

，解得n=±1，
∴直线l的方程为x=y+1或x=-y+1，
即直线l的方程为x-y-1=0或x+y-1=0．