题目内容
对n∈N*,不等式 所表示的平面区域为Dn,把Dn内的整点(横坐标与纵坐标均为整数的点)按其到原点的距离从近到远排成一列点:(x1,y1),(x2,y2),(x3,y3),…,(xn,yn).
所表示的平面区域为Dn,把Dn内的整点(横坐标与纵坐标均为整数的点)按其到原点的距离从近到远排成一列点:(x1,y1),(x2,y2),(x3,y3),…,(xn,yn).(Ⅰ)求xn、yn;
(Ⅱ)若an=3n+λ·(-xn)n-1·![]() (λ为非零常数),问是否存在整数λ,使得对任意n∈N*,都有an+1>an.
(λ为非零常数),问是否存在整数λ,使得对任意n∈N*,都有an+1>an.
解:(Ⅰ)-nx+2n>0![]() x<2,
x<2,
又x>0且x∈N*,∴x=1
故Dn内的整点都落在直线x=1上且y≤n,故Dn内的整点按其到原点的距离从近到远排成的点列为:(1,1),(1,2),(1,3),…,(1,n),∴xn=1,yn=n(5分)
(Ⅱ)an=3n+λ·(-xn)n-1·![]()
=3n+λ·(-1)n-1·2n,
∴an+1-an=3n+1+λ·(-1)n·2n+1-[3n+λ·(-1)n-1·2n]
=2·3n-3λ·(-1)n-1·2n>0
∴(-1)n-1·λ<(![]() )n-1 (*)
)n-1 (*)
当n=2k-1(k=1,2,3,…)时,(*)式即为λ<(![]() )2k-2对
)2k-2对
k=1,2,3,…都成立,∴λ<1
当n=2k(k=1,2,3,…)时,(*)式即为λ>-(![]() )2k-1对k=1,
)2k-1对k=1,
2,3,…都成立,∴λ>![]()
∴![]() <λ<1,又λ≠0且λ∈Z,
<λ<1,又λ≠0且λ∈Z,
∴存在λ=-1,使得对任意n∈N*,都有an+1>an.

练习册系列答案
相关题目
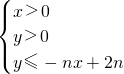 所表示的平面区域为Dn,把Dn内的整点(横坐标与纵坐标均为整数的点)按其到原点的距离从近到远排成点列:(x1,y1),(x2,y2),(x3,y3),…,(xn,yn).
所表示的平面区域为Dn,把Dn内的整点(横坐标与纵坐标均为整数的点)按其到原点的距离从近到远排成点列:(x1,y1),(x2,y2),(x3,y3),…,(xn,yn).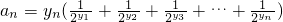 ,求数列{an}的前n项和Sn;
,求数列{an}的前n项和Sn;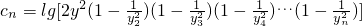 ,且数列{cn}的前n项和Tn,求T99.
,且数列{cn}的前n项和Tn,求T99.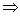 所表示的平面区域为Dn,把Dn内的整点(横坐标与纵坐标均为整数的点)按其到原点的距离从近到远排成点列:(x1,y1),(x2,y2),(x3,y4),…,(xn,yn)
所表示的平面区域为Dn,把Dn内的整点(横坐标与纵坐标均为整数的点)按其到原点的距离从近到远排成点列:(x1,y1),(x2,y2),(x3,y4),…,(xn,yn)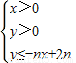 所表示的平面区域为Dn,把Dn内的整点(横坐标与纵坐标均为整数的点)按其到原点的距离从近到远排成点列:(x1,y1),(x2,y2),(x3,y3),…,(xn,yn).
所表示的平面区域为Dn,把Dn内的整点(横坐标与纵坐标均为整数的点)按其到原点的距离从近到远排成点列:(x1,y1),(x2,y2),(x3,y3),…,(xn,yn). ,求数列{an}的前n项和Sn;
,求数列{an}的前n项和Sn;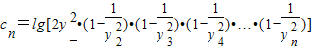 ,且数列{cn}的前n项和Tn,求T99.
,且数列{cn}的前n项和Tn,求T99.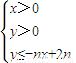 所表示的平面区域为Dn,把Dn内的整点(横坐标与纵坐标均为整数的点)按其到原点的距离从近到远排成点列:(x1,y1),(x2,y2),(x3,y3),…,(xn,yn).
所表示的平面区域为Dn,把Dn内的整点(横坐标与纵坐标均为整数的点)按其到原点的距离从近到远排成点列:(x1,y1),(x2,y2),(x3,y3),…,(xn,yn).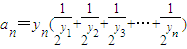 ,求数列{an}的前n项和Sn;
,求数列{an}的前n项和Sn;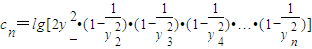 ,且数列{cn}的前n项和Tn,求T99.
,且数列{cn}的前n项和Tn,求T99.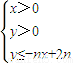 所表示的平面区域为Dn,把Dn内的整点(横坐标与纵坐标均为整数的点)按其到原点的距离从近到远排成点列:(x1,y1),(x2,y2),(x3,y3),…,(xn,yn).
所表示的平面区域为Dn,把Dn内的整点(横坐标与纵坐标均为整数的点)按其到原点的距离从近到远排成点列:(x1,y1),(x2,y2),(x3,y3),…,(xn,yn). ,求数列{an}的前n项和Sn;
,求数列{an}的前n项和Sn; ,且数列{cn}的前n项和Tn,求T99.
,且数列{cn}的前n项和Tn,求T99.